Question
Question: The figure shows a 3D view of a metal nut. The metal nut has two regular hexagonal faces. The side o...
The figure shows a 3D view of a metal nut. The metal nut has two regular hexagonal faces. The side of a hexagonal face is 2 cm and a thickness of 1 cm. A hole of diameter of 2 cm is present in the metal nut. Given the density of the metal is grams per cubic cm. Calculate the mass of this nut.
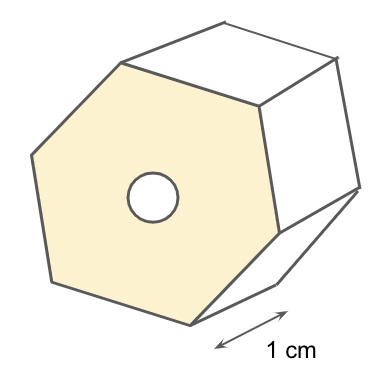
Solution
Here, we will draw a regular hexagon that can be divided into 6 equilateral triangles. Then use the formula of an equilateral triangle, 21b(2b3), where b is the side of the triangle to find the area of the each equilateral triangle with side 2 cm. Then we will find the radius from the given diameter and substitute the value of r in the formula of an area of circle, πr2, where r is a radius. We will now find the area of a metal nut by subtracting the hole drilled from t=the hexagonal face of the nut and then use the formula of density is mass by volume and we are given the density 7.9 grams per cubic cm and the above volume of metal nut to find the mass of the nut.
Complete step-by-step answer:
We know a regular hexagon can be divided into 6 equilateral triangles as shown below.
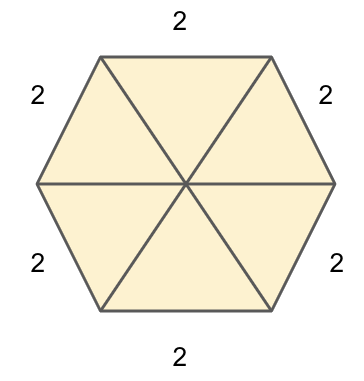
Using the formula of an equilateral triangle, 21b(2b3), where b is the side of the triangle to find the area of the each equilateral triangle with side 2 cm.
⇒212(223)=3
Since there are 6 equilateral triangles, so the area of the hexagon is 63 square cm.
We know that the hole drilled through the middle has a diameter of 2, so dividing the given diameter by 2 to find the radius.
Substituting the value of r in the formula of an area of circle, πr2, where r is a radius.
⇒π(1)2 ⇒π cm2We will now find the area of a metal nut by subtracting the hole drilled from t=the hexagonal face of the nut, we get
⇒63−π cm2
Multiplying the above area by the height of the nut, 1 cm to find the volume of the metal nut, we get
Now, we know that the formula of density is mass by volume and we are given the density 7.9 grams per cubic cm and the above volume of metal nut, we get
⇒7.9=63−πmass
Cross-multiplying the above equation, we get
Using the value of 3 and π in the above equation, we get
⇒mass=47.4(1.732)−7.9(3.142) ⇒mass=82.968−24.8186 ⇒mass=57.2706 ⇒mass≈57Hence, the mass of the nut is 57 (approx.).
Note: In solving these types of questions, students should need to understand the diagram properly to find the value of the required mass. In this question, it is very important to know the formulas of area of an equilateral triangle and that the density is the result of division of mass by volume.
