Question

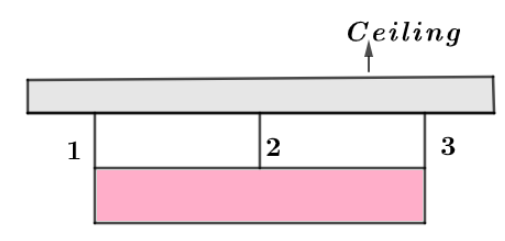
The figure shows a $300\,kg$ cylinder that is horizontal. Three steel wires support the cylinder from the ceiling. Wires $1$ and $3$ are attached at the ends of the cylinder, and wire $2$ is at the centre of the cylinder. The wires each have a cross section area of $2.0 \times {10^{ - 6}}\,{m^2}$ .Initially (before the cylinder was put in place) wires $1$ and $3$ were $2.0000\,m$ long and wire $2$ was $6.0\,mm$ longer than that. Now (with the cylinder in place) all three wires have been stretched. What are the tensions in (a) wire $1$ ? And (b) wire $2$ ? (Elasticity of steel is $E = 200 \times {10^9}\,N{m^{ - 2}}$ )

Answer 1

In order to find tensions in wires , we need to balance the all forces acting on three wires and weight acting on ceiling in downward direction and in order to achieve the same length in all three wires their change in length must be the same.

Complete step by step answer:
Let ${F_1}$ , ${F_2}$ and ${F_3}$ be the tension forces on three wires respectively. And their change in length is denoted as $\Delta {L_1}$ , $\Delta {L_2}$ and $\Delta {L_3}$ .Now, balancing all three forces with force of gravity as;
${F_1} + {F_2} + {F_3} = 300 \times 9.8$
$\Rightarrow {F_1} + {F_2} + {F_3} = 2940$
And also, ${F_1} = {F_3}$ so we can write,
${F_2} = 2940 - 2{F_1} \to (i)$
And we also know that, from modulus of elasticity of steel as given
${F_1} = {F_3} = {F_2} + \dfrac{{dAE}}{L}$
$\Rightarrow {F_1} = {F_2} + \dfrac{{dAE}}{L}$

Put, the value of ${F_2}$ from equation $(i)$ in above equation, we get
$3{F_1} = 2940 + \dfrac{{dAE}}{L} \to (ii)$
Here we have given that,
$d = 6\,mm = 0.006\,m$
$\Rightarrow A = 2 \times {10^{ - 6}}\,{m^2}$
$\Rightarrow E = 200 \times {10^9}\,N{m^{ - 2}}$
$\Rightarrow L = 2\,m$
On putting these parameters value in equation $(ii)$ we get,
$3{F_1} = 2940 + \dfrac{{6 \times 2 \times 200}}{2}$
$\Rightarrow 3{F_1} = 2940 + 1200$
$\Rightarrow {F_1} = \dfrac{{4140}}{3}$
$\therefore {F_1} = 1380\,N$

Hence tension in the wire $1$ is ${F_1} = 1380\,N$.

(b) Now, simply from equation $(i)$ we have,
${F_2} = 2940 - 2{F_1}$
Put ${F_1} = 1380\,N$ in above equation we get,
${F_2} = 2940 - 2760$
$\therefore {F_2} = 180\,N$

Hence, the tension in wire $2$ is ${F_2} = 180N$.

Note: Remember, all the tension forces on three wires are acting in the upward direction and the weight of the cylinder is downward direction. And the ceiling is in equilibrium state that’s why changes in all three wires length will be the same and hence balancing the wires and cylinder. Also $g = 9.8m{\sec ^{ - 2}}$ and $1mm = {10^{ - 3}}m$.