Question
Question: The figure shows a \(2.0\,V\) potentiometer used for the determination of internal resistance of a \...
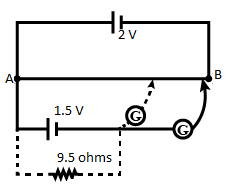
The figure shows a 2.0V potentiometer used for the determination of internal resistance of a 1.5V cell. The balance point of the cell in the open circuit is 76.3cm. When a resistor of 9.5Ω is used in the external circuit of the cell, the balance point shifts to 64.8cm length of the potentiometer. The internal resistance of the cell is:
(A) 1.63Ω
(B) 1.66Ω
(C) 1.69Ω
(D) 1.72Ω
Solution
Hint The internal resistance of the potentiometer can be determined by using the internal resistance formula of the potentiometer. The internal resistance is depending on the resistance of the resistor, distance of the two balance points in the potentiometer.
Useful formula
The expression for the internal resistance of a cell in potentiometer is given by,
r=R(l2l1−1)
Where, r is the internal resistance of the cell in the potentiometer, R is the resistance of the resistor, l1 is the distance of the initial balance point and l2 is the distance of the final balance point.
Complete step by step solution
Given that,
The voltage of the potentiometer is, V=2.0V,
The balance point of the cell in open circuit is, l1=76.3cm,
The balance point shifts to the length of the potentiometer is, l2=64.8cm.
The resistance of the resistor is, R=9.5Ω
Now,
The expression for the internal resistance of a cell in potentiometer is given by,
r=R(l2l1−1)..................(1)
By substituting the resistance of the resistor, the length of the balance point of the cell in open circuit and the balance point shifts to length of the potentiometer in the above equation (1), then the above equation (1) is written as,
r=9.5(64.876.3−1)
By dividing the terms in the above equation, then
r=9.5(1.178−1)
By subtracting the terms in the above equation, then
r=9.5(0.178)
By multiplying the terms in the above equation, then
r=1.69Ω
Hence, the option (C) is the correct answer.
Note The internal resistance of a cell is directly proportional to the resistance of the resistor and the ratio of the length of the balancing point. If the resistance of the resistor is increasing, the internal resistance of the cell is also increasing.
