Question

The figure shown above represents a modern painting that consists of four differently coloured rectangles, each of which has length l and width w. If the area of the painting is 4800 square inches, what is the width, in inches, of each of the four rectangles?

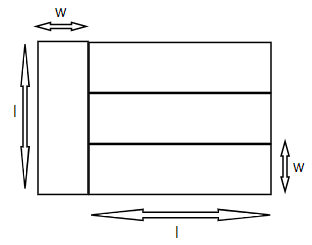
(a) 15
(b) 20
(c) 25
(d) 30
(e) 40

Answer 1

Hint: To solve this problem, it is important to know the basics of geometry particularly with respect to rectangles. Further, we will also use the formula of rectangle given by –
Area = a $\times$ b (a and b are the respective sides of the rectangle)
We will use this to solve this problem.

Complete step-by-step answer:

For solving this problem, we will refer to the figure below. We will calculate the area of the rectangle

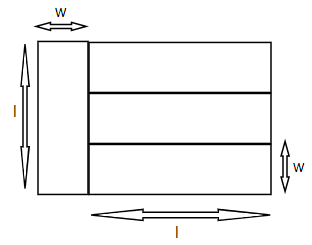
using two different methods and then equate them to find the respective values of length and width of this rectangle. The length of the larger rectangle is clearly (l+w) and the width is l (by geometry). The area is thus given by l(l+w). Another way to calculate the area of the larger rectangles is by adding up the areas of the four smaller rectangles of length l and width w. Thus, the area of the larger rectangle is 4lw (since it is made up of 4 smaller rectangles). Thus, the area is given as 4800 square inches. Thus, we have,
l(l+w) = 4lw = 4800
Thus, l(l+w) = 4lw
l+w = 4w
l = 3w --(1)
Now, we know that 4lw = 4800
Putting the results of (1) in this equation, we get,
4(3w) (w) = 4800
${{w}^{2}}=400$
w = 20 inches (we neglect the negative value since the width can never be negative)
Hence, the correct answer is (b) 20.

Note: Another way to solve the problem is to use geometry to simplify the problem. We can see that by the figure of the larger rectangle, the width of the larger (l) can be seen as the equivalent of 3 times the width of the smaller rectangle (w). This is because 3 smaller rectangles exactly fit side by side as shown in the figure. Now, we can see that l = 3w. Thus, we can directly proceed by writing the area as 4lw = 4800 and proceed by substituting l = 3w.