Question
Question: The figure showed a network of five capacitors connected to a \(100V\) supply. Calculate the total e...
The figure showed a network of five capacitors connected to a 100V supply. Calculate the total energy stored in the network.
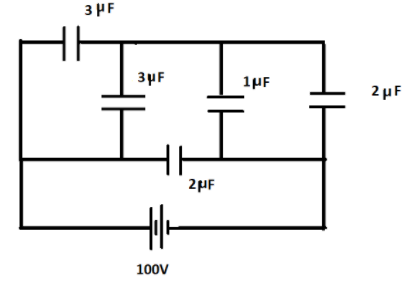
Solution
In order to solve this question, one should be aware of the concept of calculating the equivalent capacitance of the circuit. After calculating the equivalent capacitance of the circuit, put that capacitance in the formula of energy and the total energy stored in the network will be calculated. As the Potential Difference of the circuit is also given.
Complete step by step answer:
Here, the potential difference across the circuit is given.
That is, V=100V
Now, we have to calculate the capacitance of the circuit.
Here the capacitors of 3μF and 3μF are in parallel combination. Hence, their equivalent capacitance would be,
3μF+3μF=6μF
Also the capacitors of capacitance 1μF and 2μF are in parallel combination. Hence, their equivalent capacitance would be,
1μF+2μF=3μF
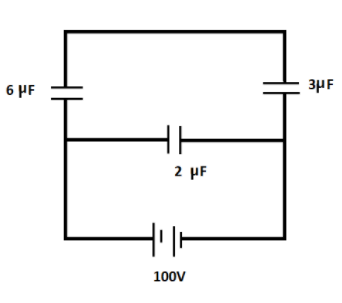
Now in the above circuit we have capacitors of capacitance 6μF and 3μF in series combination. Hence, their equivalent capacitance would be,
C′1=6μF1+3μF1
On solving, we get
C′=2μF
Now we have these two capacitors of capacitance 2μF and 2μF in parallel combination. Hence, their equivalent resistance would be,
C=2μF+2μF
Hence we get the total capacitance of the circuit as,
C=4μF
Now, the energy stored in the circuit is given by
E=21CV2
Here, C is the capacitance of the circuit.
V is the voltage drop across the circuit.
Here in this question we are given with V and that is,
V=100V
Also, we just have calculated the capacitance as C=4μF .
Putting the values of V and C in the energy equation we have,
E=21(4×10−6)(100)2
On solving we get,
E=2×10−2J
Hence the total energy stored in the circuit is E=2×10−2J.
Note: It is important to note that in the parallel combination, the equivalent capacitance of the capacitors would be the sum of the individual capacitances. While in series combination the reciprocal of the equivalent capacitance would be equal to the sum of reciprocals of individual capacitance of the capacitors.
