Question

The figure represents the instantaneous picture of a transverse wave travelling along the negative x-axis. Choose the correct alternative(s):

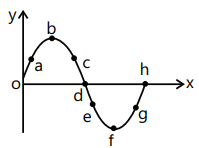
(a) The point(s) moving upwards is/are:
(b) The point(s) moving downwards is/are:
(c) The stationary point(s) is/are:
(d) The point(s) moving with maximum velocity is/are:

Answer 1

To find the solution of our question, we should be able to deduce the nature of wave just after the instant given in this question. Doing so, we can find the different velocities of all the different particles on the wave. Also, in order to find the points with maximum and minimum velocity, we analyze the wave at very certain points.

Complete step-by-step solution:
Let us first draw the nature of wave just after an instant and analyze it thoroughly:

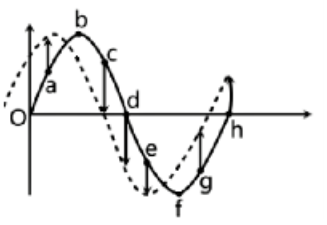
Here, as we know that any point on the wave moves only up and down, thus by understanding how the wave will look after an instant we conclude the direction of velocities of different particles.
(a) For the first part of the question, the points having upward velocities at the instant are:
Point (a), Point (g) and Point (h).
Hence, the points that are moving upwards are a, g and h.
(b) For the second part we have, the points having downward velocities at the instant are:
Point (c), Point (d) and Point (e).
Hence, the points that are moving downwards are c, d and e.
(c) For the third part we have to the stationary points.
We know for a transverse wave, the points at the Crest and the Trough of the wave are at their maximum displacement. That is, these are the places where they are at rest for an instant. Thus, the stationary points in the wave are:
Point (b) and Point (f).
Hence, the points that are stationary are (b) and (f).
(d) In the last part, to find the points with maximum velocities we use another property of wave. The particles that have zero displacement are the particles with maximum velocity. Thus, the particles with maximum velocity at the given instant of the wave is:
Point (d) and Point (h).
Hence, the points that have the maximum velocity are (d) and (h).

Note: Another method to solve the problem would be to use the wave equation and then differentiating it with respect to time to get the velocity equation of the wave. We avoided that method because of its unnecessary calculation. Problems of physics should be dealt with analogy as much as possible to save our time and widen our grip on the subject.