Question

The figure represents an experiment plot for the discharging of a capacitor in an R-C circuit. Find the range of time in which the time constant lies.

The graph between potential difference and time

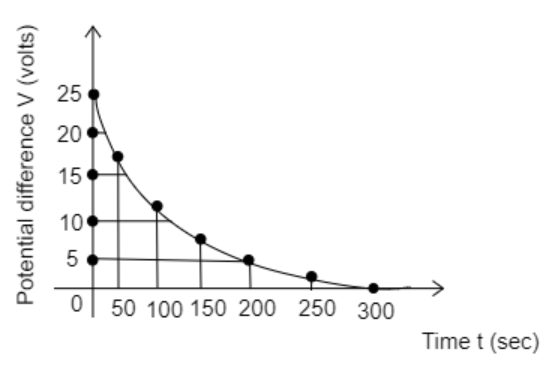
A) 0 sec and 50 sec
B) 50 sec and 100 sec
C) 100 sec and 150 sec
D) 150 sec and 200 sec

Answer 1

The figure shows that the potential difference decreases exponentially with time. The time constant in an R-C circuit refers to the time taken to charge the capacitor to 0.632 of the applied voltage. This suggests that after a time equal to the time constant the potential difference will be 0.368 of its initial voltage as the capacitor discharges.

Formula used:
-The decrease in the potential difference in an R-C circuit while discharging can be expressed as $V = {V_0}{e^{\dfrac{{ - t}}{T}}}$ where ${V_0}$ is the initial voltage before the capacitor discharges, $t$ is the time taken to discharge in seconds and $T$ is the time constant of the R-C circuit.

Complete step by step answer.
Step 1: Sketch the experiment plot given in the question and identify the initial voltage ${V_0}$ from the plot.

The graph between potential difference and time

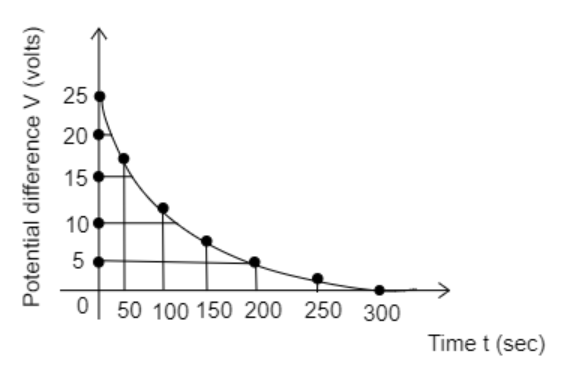
The initial voltage ${V_0}$ is the potential difference present before the capacitor discharges i.e., the value of $V$ at $t = 0{\text{sec}}$
So, from the graph, we observe that at $t = 0{\text{sec}}$, ${V_0} = 25{\text{V}}$
Step 2: Express the decrease in the potential difference $V$ .
The decrease in the potential difference during discharging of the capacitor in an R-C circuit is given by, $V = {V_0}{e^{\dfrac{{ - t}}{T}}}$ --------- (1)
where ${V_0}$ is the initial voltage before the capacitor discharges, $t$ is the time taken to discharge in seconds and $T$ is the time constant of the R-C circuit.
Here, ${V_0} = 25{\text{V}}$ then equation (1) becomes $V = 25{e^{\dfrac{{ - t}}{T}}}$ -------- (2)
Step 3: Find the time constant by substituting any value of $V$ and the corresponding value of $t$ from the graph in equation (2).
Equation (2) gives us $V = 25{e^{\dfrac{{ - t}}{T}}}$
Substitute the value of the potential difference $V = 5{\text{V}}$ and the time $t = 200{\text{sec}}$ in equation (2).
Then we have, $5 = 25{e^{\dfrac{{ - 200}}{T}}}$
Simplifying the above equation we get, $\dfrac{1}{5} = {e^{\dfrac{{ - 200}}{T}}}$
Taking the logarithm to the base $e$ on both sides we get, $- {\log _e}5 = - {\log _e}{e^{\dfrac{{200}}{T}}}$
We know, ${\log _e}5 = 1.60$ so the above equation becomes $1.60 = \dfrac{{200}}{T}$ or on rearranging we get, $T = \dfrac{{200}}{{1.60}} = 125{\text{sec}}$
$\therefore$ The time constant is $T = 125{\text{sec}}$ .

Thus the time constant lies in the time range 100 sec to 150 sec. The correct option is C.

Note: After one time constant, the capacitor must have discharged to 1−0.632 of its initial voltage. We can check if the obtained time constant is correct.
According to the statement when $t = T$ the potential difference must be $V = \left( {1 - 0.632} \right){V_0}$ .
Since ${V_0} = 25{\text{V}}$ at $t = T$, $V = \left( {1 - 0.632} \right) \times 25 = 9.05{\text{V}}$
Now, substituting $t = T$ in equation (2) we get $V = 25{e^{\dfrac{{ - T}}{T}}} = \dfrac{{25}}{e} = 9.1 \cong 9.05$
The obtained time constant is correct.