Question

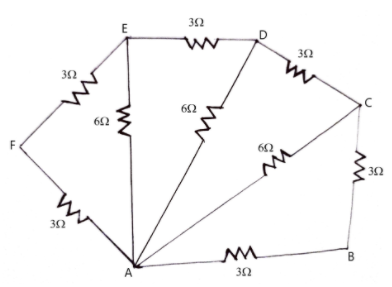
The figure given below shows a network of resistances. The effective resistance between point $A$ and point $B$ of the network is
$\begin{aligned} & A)\dfrac{3}{2}\Omega \\\ & B)6\Omega \\\ & C)3\Omega \\\ & D)2\Omega \\\ \end{aligned}$

Answer 1

When resistors are connected in series, the equivalent resistance is the sum of each resistance. When resistors are connected in parallel, reciprocal of the equivalent resistance is equal to the sum of reciprocals of each resistance. The given network of resistances is divided into triangular sections and final equivalent resistance between the given points is determined accordingly.

Formula used:
$1){{R}_{s}}={{R}_{1}}+{{R}_{2}}+.....+{{R}_{n}}$
$2)\dfrac{1}{{{R}_{p}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+....+\dfrac{1}{{{R}_{n}}}$

Complete answer: When two or more resistors are connected in series between two points in a circuit, the equivalent resistance between the two given points is the sum of each resistance. If ${{R}_{s}}$ represents the equivalent resistance of resistors connected in series between two given points in a circuit, then, ${{R}_{s}}$ is given by
${{R}_{s}}={{R}_{1}}+{{R}_{2}}+.....+{{R}_{n}}$
where
${{R}_{s}}$ is the equivalent resistance of resistors connected in series
${{R}_{1}},{{R}_{2}},.....,{{R}_{n}}$ are the resistances of $n$ individual resistors connected in series
Let this be equation 1.
Similarly, when two or more resistors are connected in parallel between two points in a circuit, the reciprocal of equivalent resistance between the two given points is the sum reciprocals of each resistance. If ${{R}_{p}}$ represents the equivalent resistance of resistors connected in parallel between two given points in a circuit, then, ${{R}_{p}}$ is given by
$\dfrac{1}{{{R}_{p}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+....+\dfrac{1}{{{R}_{n}}}$
where
${{R}_{p}}$ is the equivalent resistance of resistors connected in parallel
${{R}_{1}},{{R}_{2}},.....,{{R}_{n}}$ are the resistances of $n$ individual resistors connected in parallel
Let this be equation 2.
Coming to our question, we are provided with a network of resistors as shown in the figure given below. We are required to find the equivalent resistance between point $A$ and point $B$ of the given circuit.

To find the equivalent resistance, let us divide the network into triangles $AFE,AED,ADC$ and $ACB$.
Firstly, let us take into consideration the triangle $AFE$. From the figure, it is clear that resistor across $AF$ and resistor across $FE$ are connected in series. Using equation 1, their equivalent resistance is given by
$3\Omega +3\Omega =6\Omega$
Now, this equivalent series resistance is connected in parallel to the resistor across $AE$. Clearly, using equation 2, we have
$\dfrac{1}{{{R}_{AE}}}=\dfrac{1}{6\Omega }+\dfrac{1}{6\Omega }=\dfrac{1}{3\Omega }\Rightarrow {{R}_{AE}}=3\Omega$
where
${{R}_{AE}}$ is the equivalent resistance across $AE$
Secondly, let us consider the next triangle, $AED$. From the figure, it is clear that equivalent resistance of $AE$ and resistor across $ED$ are connected in series. Using equation 1, their equivalent resistance is given by
$3\Omega +3\Omega =6\Omega$
Now, this equivalent series resistance is connected in parallel to the resistor across $AD$. Clearly, using equation 2, we have
$\dfrac{1}{{{R}_{AD}}}=\dfrac{1}{6\Omega }+\dfrac{1}{6\Omega }=\dfrac{1}{3\Omega }\Rightarrow {{R}_{AD}}=3\Omega$
where
${{R}_{AD}}$ is the equivalent resistance across $AD$
Moving on to the next triangle $ADC$, it is clear that resistor equivalent resistance of $AD$ and resistor across $DC$ are connected in series. Using equation 1, their equivalent resistance is given by
$3\Omega +3\Omega =6\Omega$
Now, this equivalent series resistance is connected in parallel to the resistor across $AC$. Clearly, using equation 2, we have
$\dfrac{1}{{{R}_{AC}}}=\dfrac{1}{6\Omega }+\dfrac{1}{6\Omega }=\dfrac{1}{3\Omega }\Rightarrow {{R}_{AC}}=3\Omega$
where
${{R}_{AC}}$ is the equivalent resistance across $AC$
Similarly, in the next triangle $ACB$, it is clear that equivalent resistance of $AC$ and resistor across $BC$ are connected in series. Using equation 1, their equivalent resistance is given by
$3\Omega +3\Omega =6\Omega$
Now, this equivalent series resistance is connected in parallel to the resistor across $AB$. Clearly, using equation 2, we have
$\dfrac{1}{{{R}_{AC}}}=\dfrac{1}{6\Omega }+\dfrac{1}{3\Omega }=\dfrac{1}{2\Omega }\Rightarrow {{R}_{AC}}=2\Omega$
where
${{R}_{AB}}$ is the equivalent resistance across $AB$
Therefore, the equivalent resistance of the given network of resistors between point $A$ and point $B$ is equal to $2\Omega$.

Hence, the correct answer is option $D$.

Note:
When students encounter such problems in which a network of resistors are connected, it is always advisable to divide the network into different sections to determine the equivalent resistance between two given points. In the above solution, we have done the same by dividing the given network into possible triangles. If necessary, students can also redraw the given network to understand the series connections as well as the parallel connections in the network, separately and properly.