Question

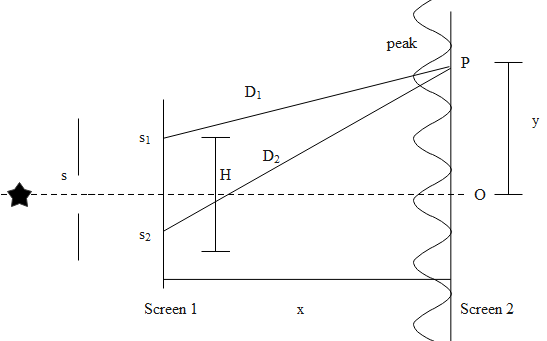
The figure drawn here, shows a modified Young’s double slit experimental set up in which
(i) State the condition for constructive and destructive interference.
(ii) Obtain the expression for fringe width
(iii) Locate the position of the central fringe.

Answer 1

The condition for the constructive and destructive interference can be obtained by using the path difference formula. The expression for the fringe width can be obtained by finding the difference between the distances of the adjacent bright fringes or the dark fringes. The position of the central fringe can be obtained by substituting the value of n as 0 in the constructive interference formula.
Formula used:
$\Delta =\dfrac{yd}{D}$

Complete step-by-step solution:
From the given information, we have the data as follows.
(i) State the condition for constructive and destructive interference.
Let the initial path difference between the slits ${{s}_{1}}$and ${{s}_{2}}$be, ${{\Delta }_{0}}=s{{s}_{2}}-s{{s}_{1}}=\dfrac{\lambda }{4}$
The path difference between the disturbance from ${{s}_{1}}$and ${{s}_{2}}$at P be, $\Delta =\dfrac{yd}{D}$
Thus, the total path difference is, ${{\Delta }_{T}}=\dfrac{\lambda }{4}+\dfrac{yd}{D}$
Thus, the condition for the constructive interference is given as follows.
${{\Delta }_{T}}=\dfrac{\lambda }{4}+\dfrac{yd}{D}=n\lambda ;\,\,\,\,\,\,n=0,1,2.......$
$\dfrac{{{y}_{n}}d}{D}=\left( n-\dfrac{1}{4} \right)\lambda$
The condition for the destructive interference is given as follows.

& {{\Delta }_{T}}=\dfrac{\lambda }{4}+\dfrac{yd}{D}=(2n-1)\dfrac{\lambda }{2} \\\ & \therefore \dfrac{y{{'}_{n}}d}{D}=\left( 2n-1-\dfrac{1}{2} \right)\dfrac{\lambda }{2} \\\ \end{aligned}$$ Thus, the condition for the destructive interference is given as follows. $$\dfrac{y{{'}_{n}}d}{D}=\left( 2n-\dfrac{3}{2} \right)\dfrac{\lambda }{2}$$ (ii) Obtain the expression for fringe width The distance between the adjacent bright fringes or the dark fringes is called the fringe width. The fringe width can be obtained by finding the difference between the distances of the adjacent bright fringes or the dark fringes. $$\begin{aligned} & \beta ={{y}_{n+1}}-{{y}_{n}} \\\ & \beta =\dfrac{(n+1)\lambda D}{d}-\dfrac{(n)\lambda D}{d} \\\ \end{aligned}$$ Thus the fringe width is represented in the mathematical expression as follows. $$\beta =\dfrac{\lambda D}{d}$$ Where $$\beta $$ is the fringe width, $$\lambda $$ is the wavelength, D is the distance between the screen and the slits and d is the distance between the slits. (iii) Locate the position of the central fringe. The position of the central fringe can be obtained by substituting the value of n as 0 in the condition for the bright fringe equation. $$\begin{aligned} & \dfrac{{{y}_{n}}d}{D}=\left( n-\dfrac{1}{4} \right)\lambda \\\ & \Rightarrow \dfrac{{{y}_{0}}d}{D}=\left( 0-\dfrac{1}{4} \right)\lambda \\\ & \therefore {{y}_{0}}=-\dfrac{\lambda D}{4d} \\\ \end{aligned}$$ $$\therefore $$ (i) The condition for constructive and destructive interference is $$\dfrac{{{y}_{n}}d}{D}=\left( n-\dfrac{1}{4} \right)\lambda $$and $$\dfrac{y{{'}_{n}}d}{D}=\left( 2n-\dfrac{3}{2} \right)\dfrac{\lambda }{2}$$. (ii) The expression for fringe width is $$\beta =\dfrac{\lambda D}{d}$$(iii) The position of the central fringe is $$-\dfrac{\lambda D}{4d}$$. **Note:** The constructive interference is the multiple of the wavelength, whereas, the destructive interference is the multiple of half the wavelength. The position of the central fringe is obtained to be negative, because the central fringe is obtained at a point below the point O.