Question
Question: The figure below shows a part of a circuit. If a current of \(12\,mA\) exists in the \(5k\Omega\) re...
The figure below shows a part of a circuit. If a current of 12mA exists in the 5kΩ resistor, find the currents in the other three resistors. What is the potential difference between the points A and B?
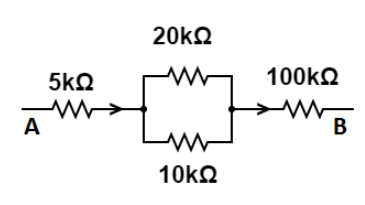
Solution
In electrical circuits, when the resistors are connected in series combination, same current flows across each resistances while when they are connected in parallel combination the potential difference is same across each resistances, we will use this concept in order to find currents in each resistors and potential difference across point A and B.
Formula used:
Net resistance between two resistances in series combination is calculated as Rseries=R1+R2
Net resistance between two resistances in parallel combination is calculated as Rparallel1=R11+R21
Current and potential difference across the resistor is related as I=RV.
Complete step by step answer:
Firstly, let us find the net resistance among the parallel combination of resistances 20kΩ(and)10kΩ using the formula Rparallel1=R11+R21 let net resistance among 20kΩ(and)10kΩ denoted as R20,10 so we have,
R20,101=201+101
⇒R20,101=20030
⇒R20,10=320kΩ
Now, we have three resistances which are connected in series with each other of resistances R20,10=320kΩ , 5kΩ and 100kΩ
now, it’s given that current of 12mA flows across the 5kΩ resistance , and since three resistances of R20,10=320kΩ , 5kΩ and 100kΩ are connected in series to each other which means same current of 12mA will flow across each resistance such that current across 100kΩ will also be 12mA. And current across R20,10=320kΩ will be 12mA,
Now, we have the resistance R20,10=320kΩ is a parallel combination of 20kΩ(and)10kΩ so, net potential difference across R20,10=320kΩ will be same in the individual resistances 20kΩ(and)10kΩ.
Let V20,10 is potential difference across the R20,10=320kΩ with current of 12mA so, using I=RV we have,
V20,10=320kΩ×12mA
⇒V20,10=80V
Now, current across the resistance 20kΩ with potential difference of V20,10=80V can be found as:
I=2080
⇒I=4mA
Similarly, the current in the 10kΩ resistance with potential difference of V20,10=80V can be found as:
I=1080
⇒I=8mA
Now, in order to find net potential difference between point A and B, we have the net current is flowing of 12mA in the series combination of resistances R20,10=320kΩ , 5kΩ and100kΩ.
Let RAB denote the net resistance between point A and B then it’s calculated as:
RAB=320+100kΩ+5kΩ
⇒RAB=121.67kΩ
Now, potential difference can be calculated by
VAB=RAB(12mA)
⇒VAB=121.67×12
∴VAB=1460.04V
Hence, the current in the other three resistances of 20kΩ,10kΩ(and)100kΩ is 4mA,8mA(and)12mA respectively.
The potential difference across the points A and B is VAB=1460.04V.
Note: It should be remembered that, the basic unit of conversions as 1mA=10−3A which is a unit of current and the unit 1kΩ=103Ω which is a unit of resistance, and the formula between potential difference, current and resistance I=RV is known as the Ohm’s law. Resistance is the property of resistors to oppose the flow of current across them in the electrical circuits.
