Question

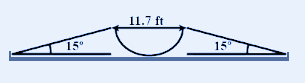
The figure below shows a $11.7\,ft$ wide ditch with the approach roads at an angle of ${15^ \circ }$ with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?

Answer 1

The motion of the bike once it climbs and jumps from the first ramp can be treated as projectile motion under the influence of gravity. The projectile should cover at least the distance between the two ramps so that the bike can land safely.

Formula used:
Range of a projectile $R = \dfrac{{{u^2}\sin 2\alpha }}{g}$where $u$is the velocity of the bike when it exits the first ramp, $\alpha$ is the angle formed by the ramps with the horizontal, $g = 32.2ft/{s^2}$ is the acceleration due to gravity.

Complete step by step solution:
We’ve been given that:
Width of the ditch is $11.7\,ft$.
To cross the ditch safely, the bike must cover the width of the ditch safely. Since both the ramps are at the same level, the bike can be considered as a projectile once it exits the first ramp.
If the projectile has a range that is equal to the length of the ditch, the bike can safely cross the ditch and land on the other side. We know that the horizontal distance covered by a projectile i.e. the Range $R$can be calculated as:
$R = \dfrac{{{u^2}\sin 2\alpha }}{g}$
Since the bike needs to have a range of $11.7{\text{ }}ft$, we can calculate the velocity with which the bike should be moving when it exits the first ramp to cover this ditch as:
${u^2} = \dfrac{{Rg}}{{\sin 2\alpha }}$
Taking the square root on both sides, we get:
$u = \sqrt {\dfrac{{Rg}}{{\sin 2\alpha }}}$
Substituting the values and solving we get,
$u = \sqrt {\dfrac{{11.7 \times 32.2}}{{\sin (2 \times {{15}^ \circ })}}} \\\ = \sqrt {\dfrac{{376.74}}{{1/2}}} \\\ = 27.44\,ft/s \\\$
$\therefore u = 27.44ft/s$
Thus, the bike should be moving with a velocity of $27.44\,ft/s$ to safely cross the ditch.

Note:
Even if the ramps are at a certain height above the ground, since their ends are at the same height level, we should notice that the ends of the ramps are the beginning and the final point of our projectile motion. In practical scenarios however, the bike cannot be treated as a point object and both the tyres of the bike should reach the other ramp for the bike to cross the ramp safely. Also we have neglected air resistance which can oppose the motion of the bike.