Question

The figure below an oscillating system of two blocks and a spring. The horizontal surface is smooth and the contact between the blocks in rough with coefficient of static friction µ. Considering that the blocks of mass m is always stationary relative to M. choose the correct option regarding the statement below.

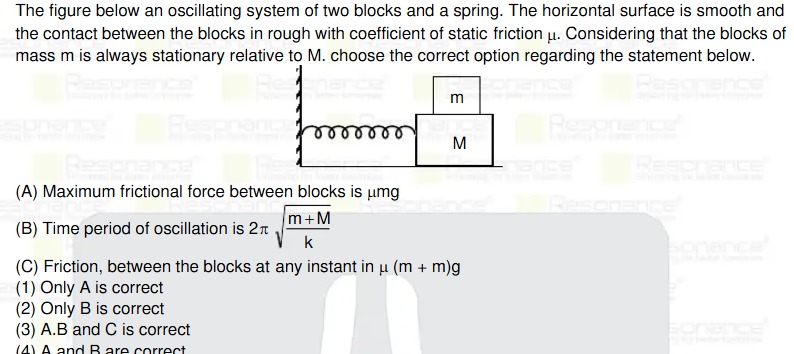
• A. Maximum frictional force between blocks is µmg
• B. Time period of oscillation is $2\pi \sqrt{\frac{m+M}{k}}$
• C. Friction, between the blocks at any instant in µ (m + m)g
• D. Only A is correct
• E. Only B is correct
• F. A.B and C is correct
• G. A and B are correct

Answer 1

Answer: (A), (B), (G)

A and B are correct.

Answer 2

1. Friction Maximum:
   For the top block of mass $m$ not to slip, the maximum static friction available is

   $$f_{\text{max}} = \mu N = \mu mg.$$

   Hence, statement (A) is correct.

2. Time Period Analysis:
   Since block $m$ always moves with block $M$, the effective inertial mass of the system is $m + M$. The restoring force is given by the spring force $-kx$. Therefore, the equation of motion becomes

   $$(m+M) \ddot{x} = -kx,$$

   leading to a time period

   $$T = 2\pi \sqrt{\frac{m+M}{k}}.$$

   This confirms that statement (B) is correct.

3. Statement (C):
   The claim in (C) about the friction being equal to $\mu(m+m)g = 2\mu mg$ at any instant is incorrect because the friction force only needs to provide the required acceleration $a$ (i.e., $f = ma$) and cannot exceed $\mu mg$.

Thus, only statements (A) and (B) are correct.