Question

The extremities of a diagonal of rectangle are (-4, 4) and (6, -1). A circle circumscribes the rectangle and cuts an intercept AB on the y-axis. Find the area of the triangle formed by AB and tangents to the circle at A and B.

Answer 1

We try to find the equation of the circle using the extremum of the diameter. From the equation we find out the intersecting points of the circle on the y-axis. Using those points, we find out the tangents at those points and their intersecting point. We got the vertices of the triangle, whose area we need to find. We use the area theorem of triangles to find the solution.

Complete step-by-step answer:
The circle is circumscribing the rectangle. So, every vertex is on the perimeter of the circle.
The points of the diagonal ends are M (-4, 4) and N (6, -1).
We know that a circle circumscribing its diameter acts as the diagonal.
So, the MN will be the diameter of the circle.
When we have two extremities of a diameter as $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ then the equation of the circle is $\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left( y-{{y}_{2}} \right)=0$.
We put the value of the points of M and N and get $\left( x+4 \right)\left( x-6 \right)+\left( y-4 \right)\left( y+1 \right)=0$.
So, the equation of the circle is ${{x}^{2}}-2x+{{y}^{2}}-3y=28$. So, the centre is $O\equiv \left( 1,\dfrac{3}{2} \right)$.

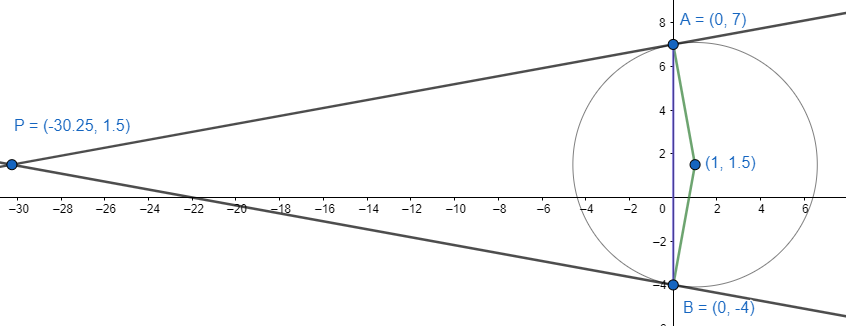
This circle cuts an intercept AB on the y-axis.
There will be 2 points on the y axis. So, we put $x=0$ in the equation to find the points A and B.
$\begin{aligned} & \left( x+4 \right)\left( x-6 \right)+\left( y-4 \right)\left( y+1 \right)=0 \\\ & \Rightarrow 4\times \left( -6 \right)+{{y}^{2}}-3y-4=0 \\\ & \Rightarrow {{y}^{2}}-3y-28=0 \\\ & \Rightarrow \left( y-7 \right)\left( y+4 \right)=0 \\\ & \Rightarrow y=7,-4 \\\ \end{aligned}$
Putting the value, we get two values of y. So, the points are $A=\left( 0,7 \right)$ and $B=\left( 0,-4 \right)$.
We draw two tangents at those two points A and B.
Equation of a line with two points is $y=\dfrac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}}x+C$.
The equation of the radius AO is $y=\dfrac{7-\dfrac{3}{2}}{0-1}x+c\Rightarrow y=-\dfrac{11}{2}x+c$.
The multiplication of the slopes of the tangent and the normal is -1.
So, the equation of tangent will be $y=\dfrac{2}{11}x+c$. It passes through point $A=\left( 0,7 \right)$.
Putting the value, we get $y=\dfrac{2}{11}x+7$. This is the tangent through $A=\left( 0,7 \right)$.
The equation of the radius BO is $y=\dfrac{-4-\dfrac{3}{2}}{0-1}x+k\Rightarrow y=\dfrac{11}{2}x+k$.
The multiplication of the slopes of the tangent and the normal is -1.
So, the equation of tangent will be $y=-\dfrac{2}{11}x+k$. It passes through point $B=\left( 0,-4 \right)$.
Putting the value, we get $y=-\dfrac{2}{11}x-4$. This is the tangent through $B=\left( 0,-4 \right)$.
We got two tangents. We find the intersecting points.
So, equating y of those two tangents we get $\dfrac{2}{11}x+7=-\dfrac{2}{11}x-4\Rightarrow \dfrac{4}{11}x=-11\Rightarrow x=\dfrac{-121}{4}$.
Putting value of x we get $y=-\dfrac{2}{11}\left( \dfrac{-121}{4} \right)-4\Rightarrow y=\dfrac{3}{2}$. The point of intersection is $P\left( \dfrac{-121}{4},\dfrac{3}{2} \right)$.
So, we need to find the area of the triangle formed by AB and tangents to the circle at A and B which is an area of $\Delta PAB$.
The area of a triangle with three vertices $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$ be $\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$ sq. unit.
So, for $\Delta PAB$ with vertices $P\left( \dfrac{-121}{4},\dfrac{3}{2} \right)$, $A=\left( 0,7 \right)$, $B=\left( 0,-4 \right)$ is $\dfrac{1}{2}\left| \dfrac{-121}{4}\left( 7+4 \right) \right|=\dfrac{1331}{8}$ sq. unit.
The area is $\dfrac{1331}{8}$ sq. unit.

Note: We can also use the theorem of geometry. We use that the tangents drawn from an external point on the circle are always of equal length. To find the tangent’s slope we just took the negative inverse of the slope of the normal. At the time of finding the are we and two values of x as 0. So, we only used it once to get the solution easily.