Solveeit Logo
Login

Question

Question: The extreme values of cos x are: (a) \[\dfrac{\sqrt{3}}{2}\text{ and }\dfrac{1}{\sqrt{2}}\] (b) ...

The extreme values of cos x are:
(a) 32 and 12\dfrac{\sqrt{3}}{2}\text{ and }\dfrac{1}{\sqrt{2}}
(b) – 1 and 0
(c) – 1 and 1
(d) 0 and 1

Explanation

Solution

Hint: Find a few points on the positive x-axis and few points on the negative x-axis and plot them. As cos x is periodic, first plot the graph of cos x and then find the maximum, minimum from that. These are the extreme values which are the required result of the question.

Complete step-by-step answer:
Extreme Values: The maximum and minimum value of the function in its range are called extreme values of the function. We need a graph of the function to solve this question.
The value of cos x at x = 0 can be given as:
cos⁡(0)=1\cos \left( 0 \right)=1
The value of cos x at x=π6,x=\dfrac{\pi }{6}, can be given as:
cos⁡(π6)=32\cos \left( \dfrac{\pi }{6} \right)=\dfrac{\sqrt{3}}{2}
The value of cos x at x=π4,x=\dfrac{\pi }{4}, can be given as:
cos⁡(π4)=12\cos \left( \dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}
The value of cos at x=π3,x=\dfrac{\pi }{3}, can be given as:
cos⁡(π3)=12\cos \left( \dfrac{\pi }{3} \right)=\dfrac{1}{2}
The value of cos x at x=π2,x=\dfrac{\pi }{2}, can be given as:
cos⁡(π2)=0\cos \left( \dfrac{\pi }{2} \right)=0
The value of cos x at x=−π6,x=\dfrac{-\pi }{6}, can be given as:
cos⁡(−π6)=32\cos \left( \dfrac{-\pi }{6} \right)=\dfrac{\sqrt{3}}{2}
The value of cos x at x=−π4,x=\dfrac{-\pi }{4},can be given as:
cos⁡(−π4)=12\cos \left( \dfrac{-\pi }{4} \right)=\dfrac{1}{\sqrt{2}}
The value of cos x at x=−π3,x=\dfrac{-\pi }{3}, can be given as:
cos⁡(−π3)=12\cos \left( \dfrac{-\pi }{3} \right)=\dfrac{1}{2}
The value of cos x at x=−π2,x=\dfrac{-\pi }{2}, can be given as:
cos⁡(−π2)=0\cos \left( \dfrac{-\pi }{2} \right)=0
So, cos x in the range of (π2,π)\left( \dfrac{\pi }{2},\pi \right) repeats as the (0,π2)\left( 0,\dfrac{\pi }{2} \right) but negative way. And in the range (−π2,−π)\left( \dfrac{-\pi }{2},-\pi \right) repeats as (π2,0)\left( \dfrac{\pi }{2},0 \right) in a negative way and it is periodic. So, we can plot it as:

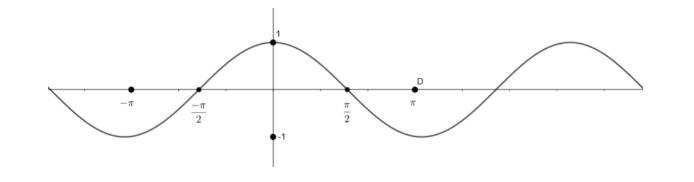
As you can see the graph always lies between – 1 and 1. So, the extreme values are – 1, 1.
Therefore, option (c) is the right answer.

Note: Be careful while plotting each and every point because even a mistake at one point may affect the whole shape of the graph. While checking the extreme values, take care that you cover the whole range because even after some values, it further crosses it, and then the answer might be wrong.