Question

The expression $[x + (x^3 - 1)^{1/2}]^5 = [x - (x^3 - 1)^{1/2}]^5$ is a polynomial of degree

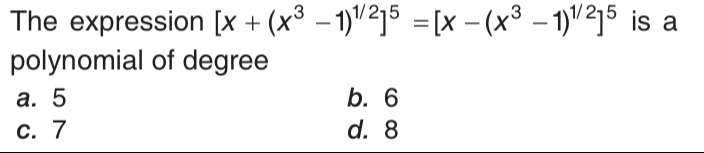
• A. 5
• B. 6
• C. 7
• D. 8

Answer 1

Answer: (B)

6

Answer 2

Let $A = x + (x^3 - 1)^{1/2}$ and $B = x - (x^3 - 1)^{1/2}$. The equation is $A^5 = B^5$, which can be written as $A^5 - B^5 = 0$.

Expanding and simplifying $A^5 - B^5 = 0$ leads to:

$2(x^3-1)^{1/2} (x^6 + 10x^5 + 5x^4 - 2x^3 - 10x^2 + 1) = 0$

The expression is a product of $(x^3-1)^{1/2}$ and a polynomial of degree 6. The question asks for the degree of the polynomial factor, which is 6.