Question

The expression $2\sqrt{\sqrt{\log_a \sqrt[4]{ab} + \log_b \sqrt[4]{ab}} - \sqrt{\log_a \sqrt[4]{\frac{b}{a}} + \log_b \sqrt[4]{\frac{a}{b}}}} \sqrt{\log_a b}$ is equal to :

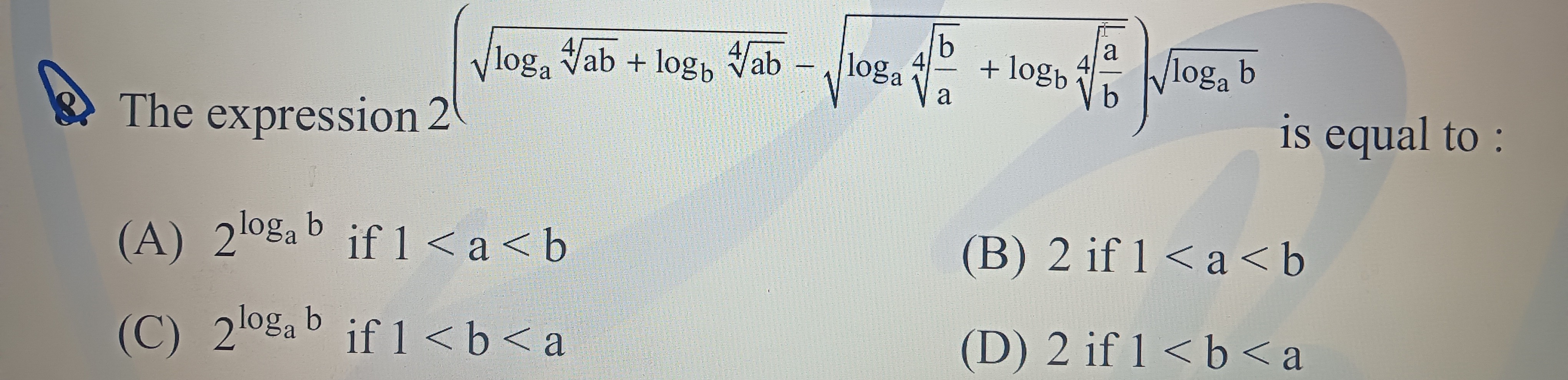
• A. $2^{\log_a b}$ if $1 < a < b$
• B. $2$ if $1 < a < b$
• C. $2^{\log_a b}$ if $1 < b < a$
• D. $2$ if $1 < b < a$

Answer 1

Answer: (B)

2 if 1 < a < b

Answer 2

Let $x = \log_a b$. We know that $\log_b a = \frac{1}{\log_a b} = \frac{1}{x}$.

First term: $T_1 = \log_a \sqrt[4]{ab} + \log_b \sqrt[4]{ab} = \frac{1}{4} (\log_a (ab) + \log_b (ab)) = \frac{1}{4} (1 + x + \frac{1}{x} + 1) = \frac{(x+1)^2}{4x}$

Second term: $T_2 = \log_a \sqrt[4]{\frac{b}{a}} + \log_b \sqrt[4]{\frac{a}{b}} = \frac{1}{4} (\log_a \left(\frac{b}{a}\right) + \log_b \left(\frac{a}{b}\right)) = \frac{1}{4} (x - 1 + \frac{1}{x} - 1) = \frac{(x-1)^2}{4x}$

Substitute these back into the expression. Let's assume the expression is $E = 2 \left( \sqrt{T_1} - \sqrt{T_2} \right) \sqrt{x}$.

$E = 2 \left( \sqrt{\frac{(x+1)^2}{4x}} - \sqrt{\frac{(x-1)^2}{4x}} \right) \sqrt{x} = |x+1| - |x-1|$

Case 1: $1 < a < b$. Then $\log_a b > \log_a a = 1$. So, $x = \log_a b > 1$. Since $x > 1$, we have: $E = (x+1) - (x-1) = 2$

Case 2: $1 < b < a$. Then $0 < \log_a b < \log_a a = 1$. So, $0 < x = \log_a b < 1$. Since $0 < x < 1$, we have: $E = (x+1) - (1-x) = 2x = 2\log_a b$

Given that option (B) matches perfectly for the first case, and the expression structure is most naturally interpreted this way, we select (B).