Question

The expansion of a mass $m$ of an ideal gas at a constant pressure $P$ is shown by the line H. The expansion of a mass $2m$ of the same gas at a pressure $\dfrac{P}{2}$ is shown by.

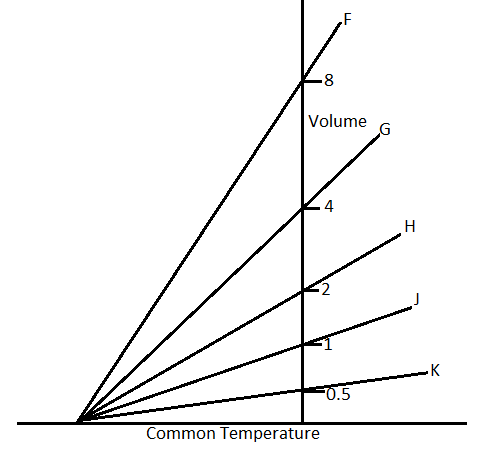
(A) Line F
(B) Line G
(C) Line H
(D) Line J or line K

Answer 1

Hint To solve this question, we need to use the ideal gas law $PV = nRT$ to find the expression for the volume. Now by putting the value of mass and pressure in the first case we get the expression for volume ${V_1}$ and similarly for the second case, we find the expression of ${V_2}$ and the write it in terms of ${V_1}$. From the graph we can obtain the value of ${V_1}$ and hence the value of ${V_2}$. The line corresponding to the value of ${V_2}$ in the graph gives the answer.

Formula Used
In the solution of this question we use the formulae,
$PV = nRT$
where $P$ is the pressure of the gas, $V$ is the volume of the gas, $n$ is the number of moles, $R$ is the universal gas constant and $T$ is the temperature of the gas.
$n = \dfrac{m}{M}$ where $m$ is the mass and $M$ is the molar mass.

Complete step by step answer:
At any constant temperature $T$ from the gas equation, we have
$PV = {\text{constant}}$ which is given by $nRT$.
So in the first case, we are given the mass of an ideal gas is $m$. Hence, the number of moles for $m$ mass is given by, ${n_1} = \dfrac{m}{M}$ where $M$ is constant for any gas and the pressure is ${P_1} = P$.
So from the gas equation
${P_1}{V_1} = {n_1}RT$
$\Rightarrow {V_1} = \dfrac{{{n_1}RT}}{{{P_1}}}$
Now by substituting the values of the ${P_1}$ and ${n_1}$ in the equation, we get,
${V_1} = \dfrac{{\dfrac{m}{M}RT}}{P}$
For the second case, the mass is given by $2m$ and the number of moles is, ${n_2} = \dfrac{{2m}}{M}$ and the pressure is given by, ${P_2} = \dfrac{P}{2}$.
Therefore from the gas equation,
${P_2}{V_2} = {n_2}RT$
$\Rightarrow {V_2} = \dfrac{{{n_2}RT}}{{{P_2}}}$
So by substituting the values of ${n_2}$ and ${P_2}$ we get,
${V_2} = \dfrac{{\dfrac{{2m}}{M}RT}}{{\dfrac{P}{2}}}$
$\Rightarrow {V_2} = 4\dfrac{{\dfrac{m}{M}RT}}{P}$
As we know have already calculated, ${V_1} = \dfrac{{\dfrac{m}{M}RT}}{P}$ so by substituting this value in the equation of ${V_2}$ we get,
${V_2} = 4{V_1}$
$\Rightarrow \dfrac{{{V_2}}}{{{V_1}}} = 4$
In the question, it is said that the volume in the first case, ${V_1}$ is given by the line $H$. So from the graph, the volume ${V_1}$ is 2.
By substituting this value in the equation of ${V_2}$ we get,
${V_2} = 4{V_1}$
Putting the value of ${V_1}$ we get,
${V_2} = 4 \times 2 = 8$
According to the graph, the line F cuts the volume for ${V_2} = 8$.

Therefore, the answer will be line $F$, which is option A.

Note We can also solve this problem by taking the slope of the curve. Since
$PV = nRT$
$\Rightarrow PV \propto MT$ where $M$ is constant
So we can write,
$\Rightarrow V \propto \dfrac{M}{P}T$
So in the Volume-Temperature graph as in the question $\dfrac{M}{P}$ is the slope.
In the first case, the slope is given as 2.
For the second case, mass and pressure are $2M$ and $\dfrac{P}{2}$, respectively.
So, we get,
$V \propto \dfrac{{2M}}{{\dfrac{P}{2}}} \propto 4\dfrac{M}{P}$.
As $\dfrac{M}{P} = 2$, for the second case, the slope is $4 \times 2 = 8$.
The answer is 8.