Question
Question: The exhaustive set of values of a for which inequation $(a-1)x^2-(a+1)x+a-1\geq0$ is true $\forall x...
The exhaustive set of values of a for which inequation (a−1)x2−(a+1)x+a−1≥0 is true ∀x≥2.
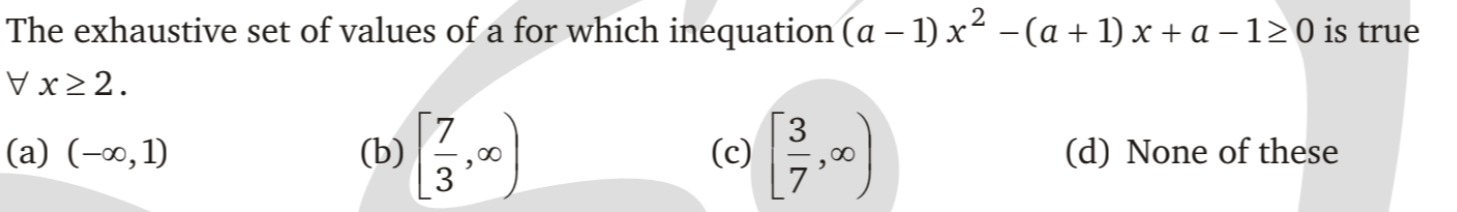
A
(−∞,1)
B
[37,∞)
C
[73,∞)
D
None of these
Answer
[$7/3, ∞)
Explanation
Solution
Let f(x)=(a−1)x2−(a+1)x+a−1. We need f(x)≥0 for all x≥2.
-
If a=1: f(x)=−2x. For f(x)≥0, we need −2x≥0⟹x≤0. This contradicts x≥2. So a=1 is not a solution.
-
If a<1: The parabola opens downwards. As x→∞, f(x)→−∞. Thus, f(x)≥0 for all x≥2 is impossible. No solutions for a<1.
-
If a>1: The parabola opens upwards.
- If D≤0: The discriminant D=−3a2+10a−3. For D≤0, we have 3a2−10a+3≥0, which gives a≤1/3 or a≥3. Since a>1, we take a≥3. In this case, f(x)≥0 for all x∈R, so it's true for x≥2.
- If D>0: This means 1/3<a<3. Combined with a>1, we have 1<a<3. For f(x)≥0 for x≥2, the roots of f(x)=0 must satisfy x1≤x2≤2. This requires two conditions:
- f(2)≥0⟹3a−7≥0⟹a≥7/3.
- Axis of symmetry xv=2(a−1)a+1≤2⟹a+1≤4a−4⟹5≤3a⟹a≥5/3. Combining 1<a<3, a≥7/3, and a≥5/3, we get 37≤a<3.
The union of solutions for a>1 is [3,∞)∪[37,3), which simplifies to [37,∞).
The exhaustive set of values for a is [37,∞).
