Question

The excess pressure inside an air bubble of radius r just below the surface of water is ${{p}_{1}}$. The excess pressure inside a drop of the same radius just outside the surface is ${{p}_{2}}$. If T is the surface tension, then:
A). ${{p}_{1}}=2{{p}_{2}}$
B). ${{p}_{1}}={{p}_{2}}$
C). ${{p}_{2}}=2{{p}_{1}}$
D). ${{p}_{2}}=0,{{p}_{1}}\ne 0$

Answer 1

Hint: For a liquid drop we have only one surface. For an air bubble we have two surfaces. Define the mathematical expression for the excess pressure inside an air bubble and inside a liquid drop using the concept of surface tension. Take their ratio to find the answer to this question.

Complete step by step answer:
Consider an air bubble of radius r and surface tension T. we have two free surfaces in an air bubble. Due to the surface tension, the molecules of the surface experience a net inward force towards the centre and normal to the surface.

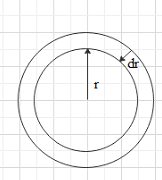
Let the outside pressure is ${{p}_{o}}$ and the inside pressure is ${{p}_{i}}$ .
So, the excess pressure will be $p={{p}_{i}}-{{p}_{o}}$
Due to the excess pressure inside the bubble will expand. Let the bubble expand by $dr$ .
So, the work done by the excess pressure will be.
$\begin{aligned} & \text{work done = force }\times \text{ displacement} \\\ & \text{work done = excess pressure }\times \text{ surface area }\times \text{ displacement} \\\ & \text{work done = p}\times \text{4}\pi {{\text{r}}^{2}}\times dr \\\ \end{aligned}$
Increase in potential energy is given by
\begin{aligned} & =\text{ surface tension }\times \text{ increase in surface area} \\\ & =\text{ }T\times \left[ 2\left\\{ 4\pi {{\left( r+dr \right)}^{2}}-4\pi {{r}^{2}} \right\\} \right] \\\ & =T\times 2\times 4\pi \times 2rdr \\\ \end{aligned}
Comparing these two equations we get that,
$\begin{aligned} & p\times 4\pi {{r}^{2}}\times dr=T\times 2\times 4\pi \times 2rdr \\\ & p=\dfrac{4T}{r} \\\ \end{aligned}$
So, the excess pressure for an air bubble will be ${{p}_{1}}=\dfrac{4T}{r}$
Again, for a liquid drop we only have one free surface. Following the same procedure, we can find that the excess pressure for liquid drop is ${{p}_{2}}=\dfrac{2T}{r}$
Taking the ratio of these two quantities,
$\begin{aligned} & \dfrac{{{p}_{1}}}{{{p}_{2}}}=\dfrac{\dfrac{4T}{r}}{\dfrac{2T}{r}}=2 \\\ & {{p}_{1}}=2{{p}_{2}} \\\ \end{aligned}$
The correct option is (A)

Note: While solving numerical related to this always remember that if we consider the a soap bubble or air bubble the excess pressure will be given as $\dfrac{4T}{r}$ and if we consider a liquid drop such as water drop the excess pressure will be given as $\dfrac{2T}{r}$.