Question

The escape velocity for a body projected vertically upwards from the surface of the earth is $11.2km{{s}^{-1}}$. If the body is projected in a direction making an angle ${{45}^{0}}$ with the vertical, then find the escape velocity.

Answer 1

Hint: Escape velocity of particle is given by ${{v}_{e}}=\sqrt{2gR}$, which is the minimum velocity of a particle by which it has to projected from earth surface so that it can escape earth’s magnetic field. In the formula of escape velocity there is no dependency on the angle by which a particle is projected. Therefore escape velocity will be the same whether it is projected vertically or inclined.

Complete step by step answer:
To know the relation of escape velocity, let us suppose an object of mass m on the earth’s surface which has to be projected upwards. Right now the object is in the presence of earth’s magnetic field, therefore we have to give the object minimum kinetic energy so that it is able to leave the earth’s magnetic field and that minimum velocity is known as escape velocity.

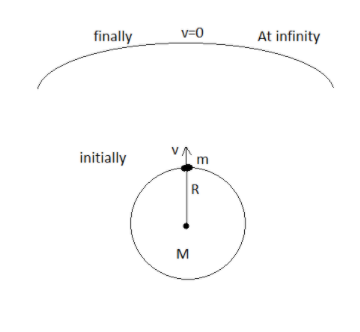
Applying the energy conservation law i.e. total initial energy = total final energy
KE = Kinetic Energy
PE = Potential Energy

& K{{E}_{i}}+P{{E}_{i}}=K{{E}_{f}}+P{{E}_{f}} \\\ & \dfrac{1}{2}m{{v}_{e}}^{2}-\dfrac{GMm}{R}=0+0 \\\ \end{aligned}$$ Kinetic Energy $$=\dfrac{1}{2}m{{v}^{2}}$$ Potential Energy $$=-\dfrac{GMm}{R}$$ Final kinetic energy is zero because the object will stop at an infinite distance from earth i.e. v=0 and Potential Energy is zero at infinity (because potential energy is inversely proportional to distance and distance becomes infinite). $$\begin{aligned} & \dfrac{1}{2}m{{v}_{e}}^{2}=\dfrac{GMm}{R} \\\ & {{v}_{e}}=\sqrt{\dfrac{2GM}{R}} \\\ \end{aligned}$$ Also we know that acceleration due to gravity $$g=\dfrac{GM}{{{R}^{2}}}$$ Therefore, we get the escape velocity in terms of acceleration due to gravity that is ${{v}_{e}}=\sqrt{2gR}$ Putting the values of g and R in the above formula we get the escape velocity on earth surface must be equals to $11.2km{{s}^{-1}}$. And as we have seen there is no relation of escape velocity to the angle of projection therefore the escape velocity always remains same and independent of projected angle. Escape Velocity: The minimum velocity by which a particle should be projected from earth’s surface, so that it can escape out from the gravitational field of earth is known as escape velocity on earth surface. Note: Students are advised in such types of questions, go through formula and find the relation that is asked in question. In this way you are able to get the correct answer. There is a reason why the atmosphere does not present a moon, now you are able to give the answer. Because the rms velocity of molecules on moon is greater than the escape velocity of moon. There all the molecules will escape and we are left with no molecules.