Question
Question: The equivalent resistance between points A and ...
The equivalent resistance between points A and
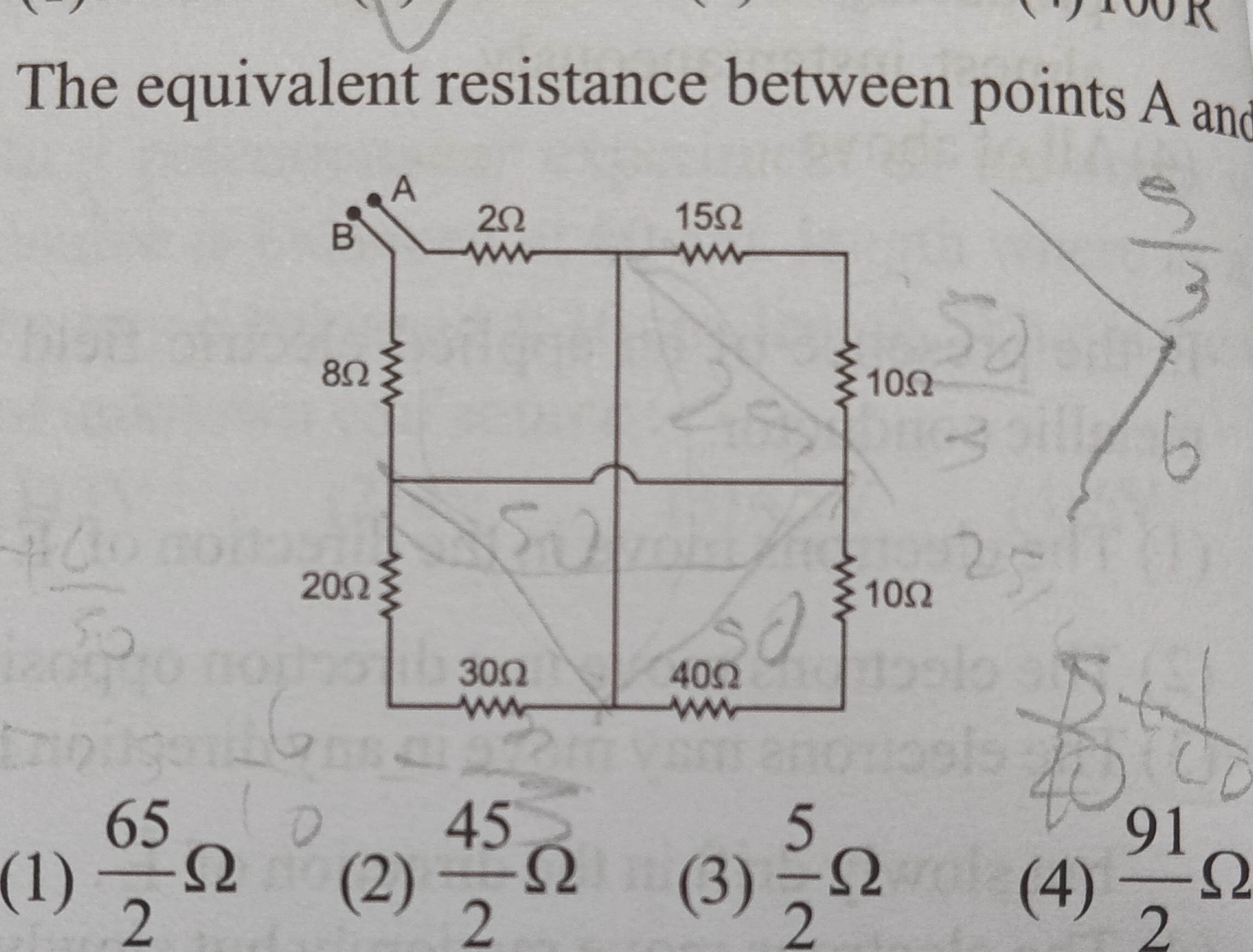
265Ω
245Ω
25Ω
291Ω
None of the options matched the calculated value.
Solution
Let's interpret the circuit diagram based on standard conventions. The circuit consists of a square-shaped arrangement of resistors with two diagonal resistors. Let the four corner nodes be: - Top-left: A - Top-right: Q - Bottom-right: R - Bottom-left: B The resistors on the perimeter of the square are: - RAQ=2Ω (between A and Q) - RQR=15Ω (between Q and R) - RRB=40Ω (between R and B) - The left side of the square has two resistors, 8Ω and 20Ω, placed one below the other. The most common interpretation for such a drawing is that they are in series, forming the left arm of the bridge. So, RBA=8Ω+20Ω=28Ω (between B and A). The diagonal resistors are: - RAR=30Ω (between A and R) - RQB=10Ω (between Q and B) This is a complex Wheatstone bridge configuration. We can solve it using Nodal Analysis. Let the potential at point B be 0V. Let the potential at point A be V. Let the potentials at nodes Q and R be VQ and VR respectively. Applying Kirchhoff's Current Law (KCL) at nodes Q and R: At Node Q: (Sum of currents leaving Q is zero) Currents leaving Q are: - To A: (VQ−V)/2 - To R: (VQ−VR)/15 - To B: (VQ−0)/10 2VQ−V+15VQ−VR+10VQ=0 Multiply by LCM(2, 15, 10) = 30: 15(VQ−V)+2(VQ−VR)+3VQ=0 15VQ−15V+2VQ−2VR+3VQ=0 20VQ−2VR=15V --- (Equation 1) At Node R: (Sum of currents leaving R is zero) Currents leaving R are: - To Q: (VR−VQ)/15 - To B: (VR−0)/40 - To A: (VR−V)/30 15VR−VQ+40VR+30VR−V=0 Multiply by LCM(15, 40, 30) = 120: 8(VR−VQ)+3VR+4(VR−V)=0 8VR−8VQ+3VR+4VR−4V=0 −8VQ+15VR=4V --- (Equation 2) Now we have a system of two linear equations: 1) 20VQ−2VR=15V 2) −8VQ+15VR=4V From Equation 1, express VR in terms of VQ: 2VR=20VQ−15V⟹VR=10VQ−215V Substitute this expression for VR into Equation 2: −8VQ+15(10VQ−215V)=4V −8VQ+150VQ−2225V=4V 142VQ=4V+2225V 142VQ=28V+225V 142VQ=2233V VQ=284233V Now, calculate VR: VR=10(284233V)−215V VR=2842330V−28415×142V VR=2842330V−2130V VR=284200V=7150V The total current I flowing from A to B is the sum of currents leaving node A: I=IA→Q+IA→R+IA→B (where IA→B is the current through the 28Ω arm directly connecting A and B) I=2V−VQ+30V−VR+28V−0 Substitute the values of VQ and VR: I=2V−284233V+30V−7150V+28V I=2284284V−233V+307171V−50V+28V I=56851V+213021V+28V I=56851V+7107V+28V To sum these fractions, find the Least Common Multiple (LCM) of the denominators (568, 710, 28). 568=8×71 710=10×71 28=4×7 LCM(568,710,28)=23×5×7×71=8×5×7×71=40×497=19880. I=V(1988051×(19880/568)+198807×(19880/710)+198801×(19880/28)) I=V(1988051×35+198807×28+198801×710) I=V(198801785+19880196+19880710) I=V(198801785+196+710) I=V(198802691) The equivalent resistance Req is IV: Req=269119880Ω Now, let's compare this calculated value with the given options: (1) 265Ω=32.5Ω (2) 245Ω=22.5Ω (3) 25Ω=2.5Ω (4) 291Ω=45.5Ω Our calculated value is Req=269119880≈7.387Ω. This value does not match any of the provided options. This suggests a potential error in the question's diagram values or the options themselves. The final answer is None of the options matched the calculated value.
