Question

The equivalent resistance between A and B will be (in ohms)

A. $\dfrac{2}{7}$
B. 8
C. $\dfrac{4}{3}$
D. $\dfrac{7}{3}$

Answer 1

In this question, we need to determine the equivalent resistance between terminal A and B in ohms. For this, we will use the property of the resistance connected in series as well as in parallel.

Complete step by step answer:
From the given circuit diagram, we can see that two resistances are connected to the node A of equal value, and so, we can say that the equal voltage drop will take place across both the resistances.
Similarly, we can see that two resistances are connected to the node B of equal value, and so, we can say that the equal voltage drop will take place across both the resistances.
Let the upper point where 3 ohms and 4 ohms meet be C so, the lower point where 3 ohms and 4 ohms meet will also be at the same potential. Hence, consider that point to be C as well.
Also, let the centre point be O.
Hence, the given circuit diagram (figure) will be reduced to

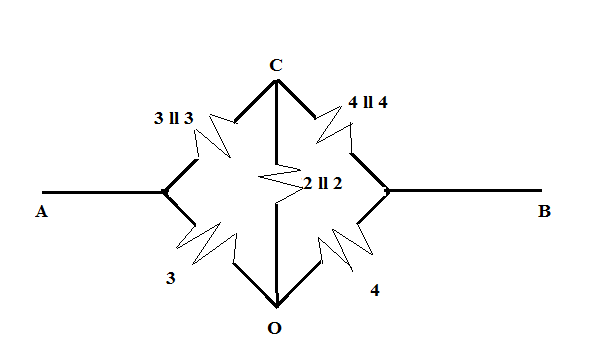
Here, the parallel equivalent of the resistances are calculated as
$3{\text{ II 3}} = \dfrac{{3 \times 3}}{{3 + 3}} = \dfrac{3}{2}$
Similarly,
${\text{4 II 4}} = \dfrac{{4 \times 4}}{{4 + 4}} = \dfrac{{16}}{8} = 2$
Again,
${\text{2 II 2}} = \dfrac{{2 \times 2}}{{2 + 2}} = \dfrac{4}{4} = 1$
So, the above-drawn figure is further reduced to

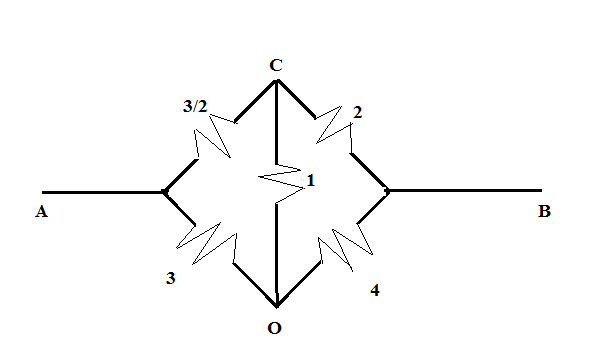
Now, from the above figure, we can see that the product of the resistances of the opposite sides of the bridge is equal such that $\dfrac{3}{2} \times 4 = 3 \times 2$. Hence, we can say that the bridge is balanced and so, no current will flow through the CO part of the circuit. Hence, the figure is further reduced to
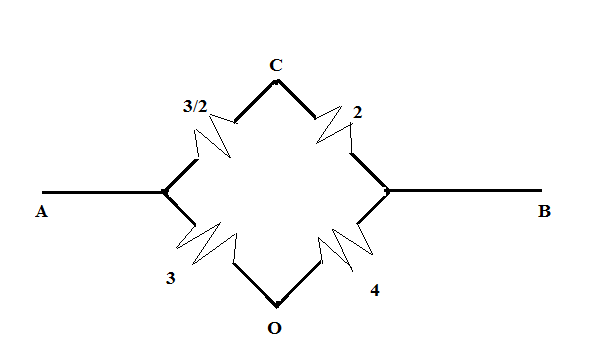Now, we can see that $\dfrac{3}{2}$, and 2 ohms are connected in parallel with the series combination of the 3 and 4 ohms.
Hence, the equivalent resistance between the terminals A and B is given as:
$R = \left( {\dfrac{3}{2} + 2} \right){\text{ ll }}\left( {3 + 4} \right) \\\ = \left( {\dfrac{7}{2}} \right){\text{ ll }}7 \\\ = \dfrac{{\dfrac{7}{2} \times 7}}{{\left( {\dfrac{7}{2} + 7} \right)}} \\\ = \dfrac{{49}}{2} \times \dfrac{2}{{14 + 7}} \\\ = \dfrac{{49}}{{21}} \\\ = \dfrac{7}{3}\Omega \\\$
Therefore, the equivalent resistance between the terminals A and B is $\dfrac{7}{3}\Omega$

So, the correct answer is “Option D”.

Note:
In the complex circuit diagram (figure), we need to simplify the circuit using parallel and series combinations of the elements until we get the equivalent resistances. Moreover, the resistances connected across the same potential points; then, the resistances are known to be parallel connected.