Question

The equivalent resistance between A and B is:

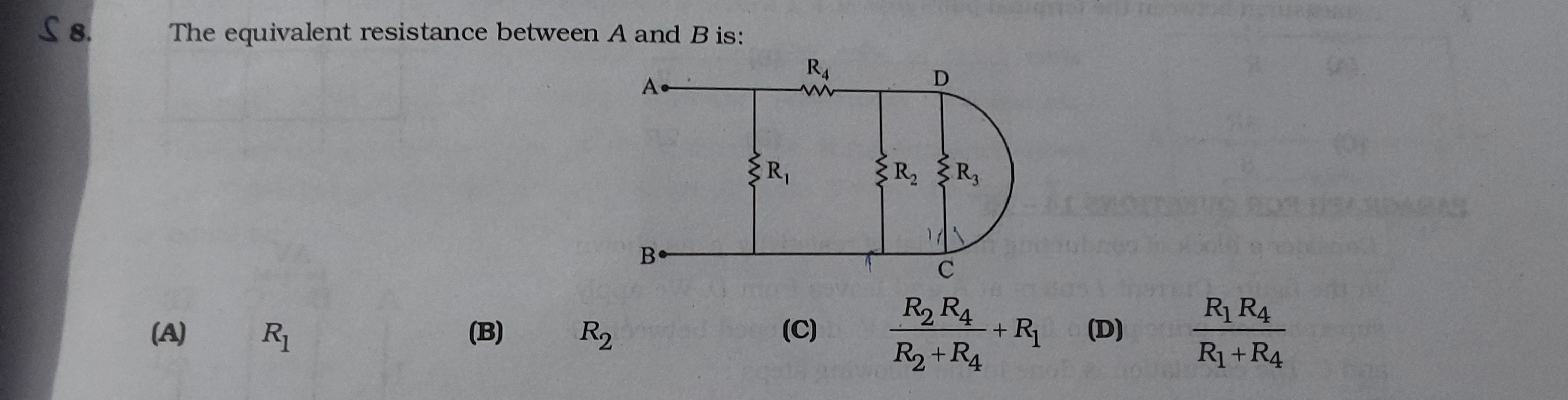
• A. $R_1$
• B. $R_2$
• C. $\frac{R_2 R_4}{R_2+R_4}+R_1$
• D. $\frac{R_1 R_4}{R_1 + R_4}$

Answer 1

Answer: (D)

(D) $\frac{R_1 R_4}{R_1 + R_4}$

Answer 2

To find the equivalent resistance between points A and B, we need to analyze the circuit. Assume R3 is a short circuit (R3 = 0). Then the parallel combination of R2 and R3 becomes:

$R_{DB} = \frac{R_2 \times 0}{R_2 + 0} = 0$

This means the resistance between D and B is zero, effectively making D and B the same electrical point.

Now, the circuit simplifies:

• R1 is connected between A and B.
• R4 is connected between A and D. Since D is now effectively B, R4 is connected between A and B.

Therefore, R1 and R4 are in parallel. The equivalent resistance between A and B would be:

$R_{AB} = \frac{R_1 R_4}{R_1 + R_4}$