Question

The equivalent resistance between A and B is:

A. $\dfrac{{8R}}{5}$
B. $\dfrac{{5R}}{8}$
C. $\dfrac{{3R}}{8}$
D. $\dfrac{{7R}}{8}$

Answer 1

To solve this question, we need to identify the series and the parallel combinations of the resistances from the arrangement of the resistances given in the figure. As we combine the resistances, the circuit will be reduced and therefore become simplified.

Complete step by step answer:
As is clearly visible in the given figure, the rightmost two resistors of $R$ resistance each are connected in the series combination. So their equivalent resistance is given by
${R_1} = R + R$
$\Rightarrow {R_1} = 2R$
So the given circuit is reduced to

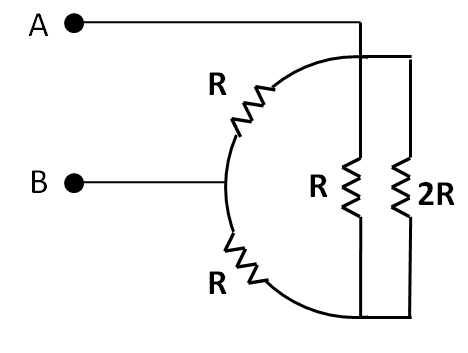
Now, we can see that the rightmost two resistors of resistances $R$ and $2R$ are connected in the parallel combination. So their equivalent resistance is given by
$\dfrac{1}{{{R_2}}} = \dfrac{1}{R} + \dfrac{1}{{2R}}$
$\Rightarrow \dfrac{1}{{{R_2}}} = \dfrac{3}{{2R}}$
Taking the reciprocal, we get
${R_2} = \dfrac{{2R}}{3}$
So, the above circuit reduces to

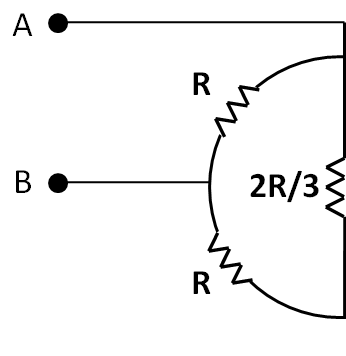
Now, let us label the bottom point as C. So the potentials across all the resistors can be shown as in the figure below.

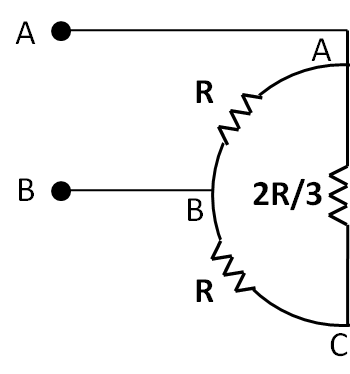
From the potentials across the resistors, we can say that the resistances of $R$ and $\dfrac{{2R}}{3}$ are connected in series combination with each other. So their equivalent resistance is given by
${R_3} = R + \dfrac{{2R}}{3}$
$\Rightarrow {R_3} = \dfrac{{5R}}{3}$
Also, this series combination is connected in parallel combination with the resistance of $R$. So the equivalent resistance is given by
$\dfrac{1}{{{R_4}}} = \dfrac{3}{{5R}} + \dfrac{1}{R}$
$\Rightarrow \dfrac{1}{{{R_4}}} = \dfrac{8}{{5R}}$
Taking the reciprocal, we finally get
${R_4} = \dfrac{{5R}}{8}$
Thus, the equivalent resistance of the given combination of the resistors between A and B is equal to $\dfrac{{5R}}{8}$.
Hence, the correct answer is option B.

Note: For identifying the series combination between two resistors, we must ensure that the current flowing through one must not be divided before reaching the other. That is, the same current must flow through both of them. And for the parallel combination between two resistors, we must ensure that they both must have the same potential difference across them.