Question

The equivalent resistance between A and B in the figure is

(A) $5\Omega$
(B) $3\Omega$
(C) $8\Omega$
(D) $4\Omega$

Answer 1

To calculate the equivalent resistance, we need to calculate the equivalent in each parallel there wires between A and B by the formula for series resistances. Then we need to calculate the equivalent resistance for the three wires by the formula for the parallel resistances.
Formula used: In this solution, we are going to use the following formula,
$\Rightarrow {R_{eq}} = {R_1} + {R_2} + {R_3} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in series.
And $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in a parallel circuit.

Complete step by step answer:
In this question, we have to find the equivalent resistance between points A and B. So we can simply draw the circuit as,

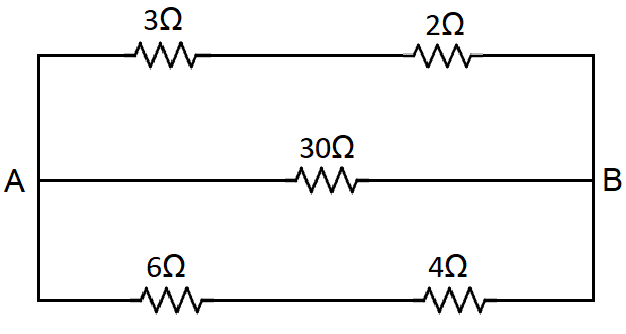
So from the figure, we can see that between points A and B there are three wires which are in parallel connection. Among them, on the topmost wire, there are two resistances which are in series connection. So on the top wire, we can find the equivalent resistance of the two resistances in series by the formula,
$\Rightarrow {R_{eq}} = {R_1} + {R_2} + {R_3} + ....$
So here ${R_1} = 3\Omega$ and ${R_2} = 2\Omega$.
Therefore, by substituting the values of ${R_1}$ and ${R_2}$, we get the equivalent resistance as,
$\Rightarrow {R_{eq1}} = 3\Omega + 2\Omega$
$\Rightarrow {R_{eq1}} = 5\Omega$
And on the bottom wire, we can see there are again two resistances in series. So we get the equivalent as,
$\Rightarrow {R_{eq2}} = 6\Omega + 4\Omega$
$\Rightarrow {R_{eq2}} = 10\Omega$
Therefore, now we can redraw the equivalent circuit as,

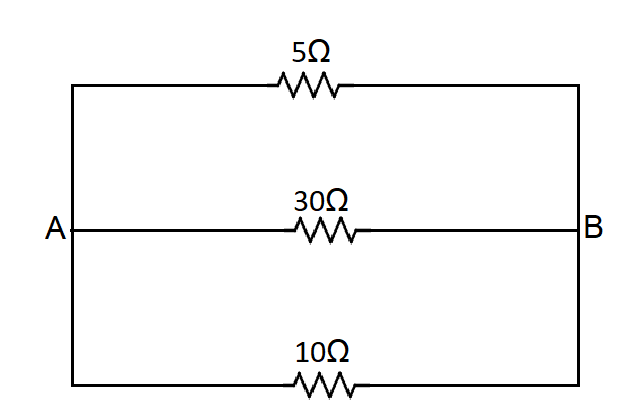
So here we can see that there are three resistances present in parallel between the points A and B. Therefore we can find the equivalent resistance as,
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$ where ${R_1} = 5\Omega$ , ${R_2} = 30\Omega$ and ${R_3} = 10\Omega$.
Now we can substitute the values of the resistances in the equation and we get,
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{5} + \dfrac{1}{{30}} + \dfrac{1}{{10}}$
We can now do the addition of the fractions as,
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{{6 + 1 + 3}}{{30}}$ where we have taken 30 as the LCM in the denominator.
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{{10}}{{30}}$
Here we can cancel out 10 from the numerator and the denominator and we get,
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{3}$
So the value of the equivalent resistance is given by the reciprocal of this answer. That is,
$\Rightarrow {R_{eq}} = 3$
So the equivalent resistance between points A and B is ${R_{eq}} = 3\Omega$.
Therefore the correct answer is (B); $3\Omega$.

Note:
In the given circuit, when the two resistances are in series condition then the current that flows in them both are the same. But when the resistances are in parallel, the potential difference is the same across the resistances but the current varies.