Question

The equivalent resistance across A and B is

A. $2\Omega$
B. $3\Omega$
C. $4\Omega$
D. $5\Omega$

Answer 1

Let's obtain a quick overview of the wheatstone principle, on which the given problem is based on. The Wheatstone bridge operates on the null deflection principle, which states that their resistance ratios are equivalent and no current flows across the circuit. When no current flows through the galvanometer, the bridge is considered to be balanced.

Complete answer:
A wheat-stone bridge is used in this setup. As a result, no current would flow through the $10\Omega$resistor.

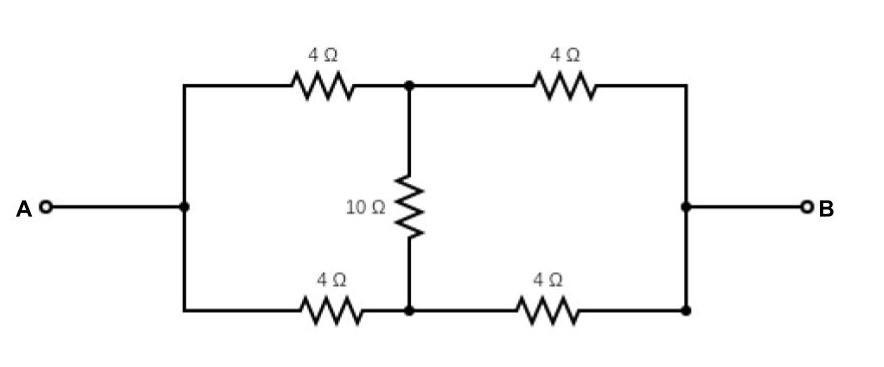
As a result, the resistance in the analogous circuit might be ignored.
We now have two branches, each with two $4\Omega$ in sequence and parallel to one another.

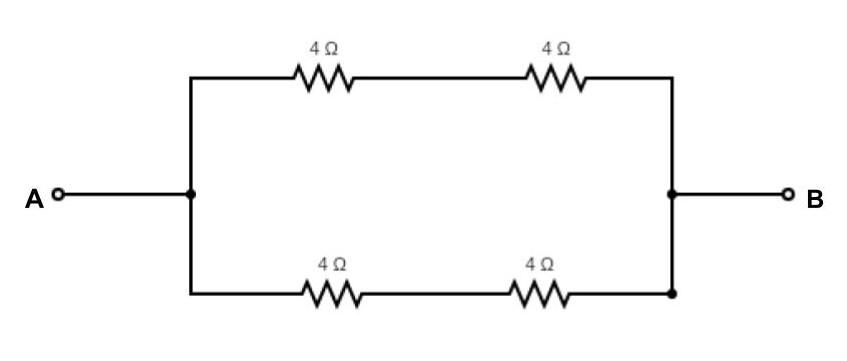
It's possible to sketch the analogous circuit as we have: $\dfrac{P}{Q} = \dfrac{R}{S}$ i.e. $\dfrac{4}{4} = \dfrac{4}{4}$
As a result, the circuit in question is a balanced Wheatstone's bridge.
As a result, the analogous resistance between points A and B is:
$\dfrac{{\left( {4 + 4} \right) \times \left( {4 + 4} \right)}}{{\left( {4 + 4} \right) \times \left( {4 + 4} \right)}} = 4\Omega$
Therefore, the equivalent resistance across A and B is $4\Omega$

So, the correct option is: (C) $4\Omega$.

Additional information:
The Wheatstone Bridge is used to carefully measure very low resistance levels. Temperature, strain, light, and other physical characteristics are measured using a Wheatstone bridge and an operational amplifier.

Note:
The Wheatstone bridge's key advantage is that it may be easily integrated into a variety of configurations. Because the results are assessed in terms of resistance and are exact and precise, the Wheatstone bridge is known as an ohmmeter. Even in m ohms', we can measure minute changes in the bridge.