Question

The equivalent inductance between A and B is:

A. $1H$
B. $4H$
C. $0.8H$
D. $16H$

Answer 1

First rearrange the figure and consider points at different intersections, label those points and then observe whether the inductances are in series combination or parallel combination. The resultant of two inductances in parallel combination is given as the inverse of the sum of their inverses. It is exactly the same as the resultant of resistors in parallel combination.

Complete step by step answer:
This circuit looks confusing. The best way to solve such problems is to simplify the given figure. Let us label the points of intersection and then calculate the effective inductance.Consider the figure below:

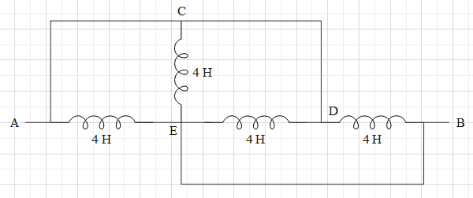
It is clear now that between point C and D, there is no inductance. So, we can remove the portion of wire between C and D and join those points. Potential drop across points A-C-D will be zero. Similarly, potential drop across E-B will also be zero.Consider the simplified figure below:

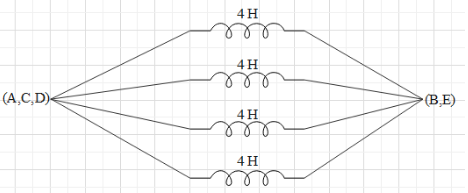
It is clear that the inductors are in parallel.
The resultant inductance will be given as:
$\dfrac{1}{{{L_{resultant}}}} = \dfrac{1}{L} + \dfrac{1}{L} + \dfrac{1}{L} + \dfrac{1}{L}$
Each inductance has value $L = 4H$
$\Rightarrow \dfrac{1}{{{L_{resultant}}}} = \dfrac{1}{4} + \dfrac{1}{4} + \dfrac{1}{4} + \dfrac{1}{4}$
$\Rightarrow \dfrac{1}{{{L_{resultant}}}} = \dfrac{4}{4}$
$\therefore {L_{resultant}} = 1H$
The equivalent inductance between A and B is $1H$ .

Therefore, option A is the correct answer.

Note: The formula to calculate effective inductance is the same for inductors and resistors for series and parallel combination. Be careful while labelling the intersection points and neglect all wires with no resistance between two points. The unit of inductance is Henry.For the inductors in series combination, the effective inductance is the arithmetic sum of all the inductances. It is again similar to the effective resistance for the resistors in series combination.