Question
Question: The equivalent capacity between A and B in the given circuit is (\[{{\text{C}}_{\text{1}}} = 4 \mu F...
The equivalent capacity between A and B in the given circuit is (C1=4μF, C2=12μF, C3=8μF, C4=4μF, C5=8μF)
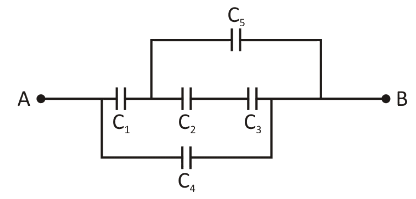
A. 24μF
B. 36μF
C. 316μF
D. 38μF
Explanation
Solution
In this question, the given figure can be represented or drawn as the balance wheatstone bridge. Find the capacitance of the upper arm and the lower arm of the circuit then by using both capacitance find the equivalent capacitance of the circuit.
Complete step by step answer:
The given figure can be redrawn into equivalent circuit as shown:
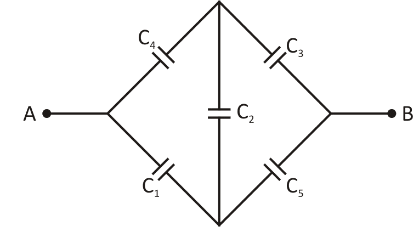
Here, the wheatstone bridge is balanced. So,12μF becomes ineffective. Capacitance of the upper arm and C3 are in series, CU1=C41+C31
Where CU is the upper arm capacitance and
C1=4μF , C2=12μF,
C3=8μF, C4=4μF, C5=8μF
