Question

The equivalent capacitance between $x$ and $y$ is:

Answer 1

When the capacitors are connected in a way that charge in each of the capacitors are the same and there is a potential difference across each of them then it is called series combination. When the capacitors are connected in a way that the charge in each capacitor is different whereas potential differences across them are the same then it is called parallel combination.

Formula used:
When the capacitors are in series combination then we have to use this formula,
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ......\dfrac{1}{{{C_n}}}$
When the capacitors are in parallel combination then we have to use this formula.
${C_{eq}} = {C_1} + {C_2} + ......{C_n}$

Complete step by step answer:
In the above question these two are connected in parallel

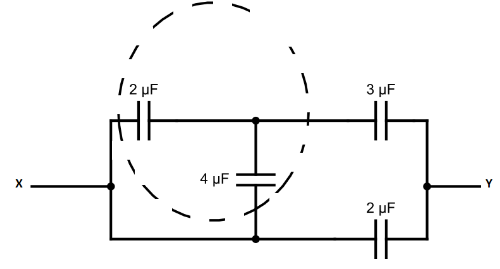
So, this circuit diagram can be drawn like this

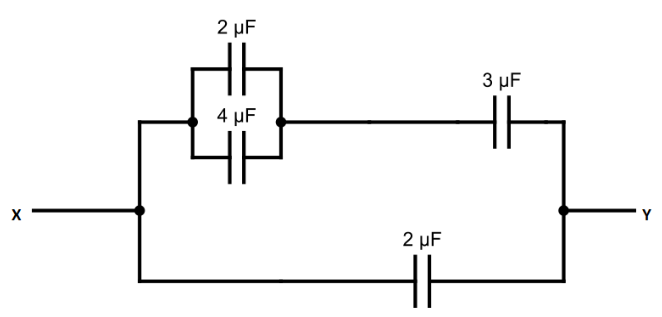
when we find ${C_{eq}}$ of these two capacitors using formula of parallel combination is
$\Rightarrow 4 + 2$
$\Rightarrow 6\mu F$
So, the circuit diagram can be drawn like this

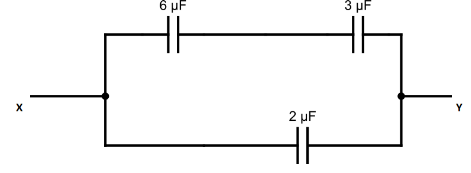
The $6\mu F$and $3\mu F$ capacitors are connected in series then ${C_{eq}}$ of these capacitors is
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{6} + \dfrac{1}{3}$
$\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{3}{6}$
$\Rightarrow {C_{eq}} = \dfrac{6}{3}$
$\Rightarrow {C_{eq}} = 2\mu F$

When we take the capacitance $2\mu F$ at the place of these two capacitors $6\mu F$and $2\mu F$then no change in equivalent capacitance so circuit can be drawn like this

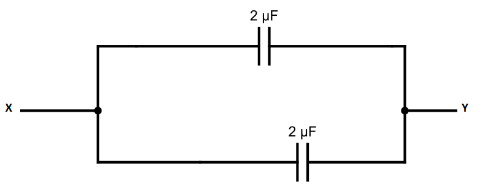
At last, we calculate ${C_{eq}}$ of these two capacitors $2\mu F$and $2\mu F$
${C_{eq}} = 2 + 2$
$\therefore {C_{eq}} = 4\mu F$

Hence, the equivalent capacitance between X and Y is $4\mu F$.

Note: If the capacitors are connected in series, then charge of each capacitor is the same and there is a potential difference across each of the capacitors.If the capacitors are connected in parallel, then charge on each capacitor is different but potential difference across each of the capacitors is the same.