Question

The equivalent capacitance between A and B is

$\left( A \right)1\mu C$
$\left( B \right)\dfrac{8}{3}\mu C$
$\left( C \right)\dfrac{9}{8}\mu C$
$\left( D \right)\dfrac{{11}}{6}\mu C$

Answer 1

Here we need to find the equivalent capacitance which we can say is the total capacitance across AB. In every step we have to make the total capacitance in each branch at every step. So as to find the solution without any mistake, first we will name each branch then find total capacitance in each branch which further solves the total capacitance across AB.

Complete step by step solution:
As per the problem we have four capacitors having capacitance $1\mu C,1\mu C,2\mu C\,{\text{and}}\,1\mu C$.
Where some are connected in series while some are connected in parallel.
Now on drawing the given figure we can see,

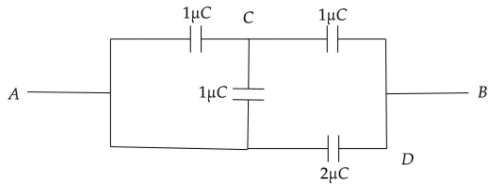
In branch CD the two capacitors are connected in series with each other.
Hence the total resistance of the branch CD we will get,
${C_{CD}} = \dfrac{{{C_1} \times {C_2}}}{{{C_1} + {C_2}}}$
Where,
${C_{CD}}$ is the total capacitance.
${C_1}$ and ${C_2}$ are conned in series capacitance equal to $1\mu C$ and $2\mu C$ respectively.
Now putting the known values in the above equation we will get,
${C_{CD}} = \dfrac{{1\mu C \times 2\mu C}}{{1\mu C + 2\mu C}} = \dfrac{2}{3}\mu C$
Now the circuit will look like,

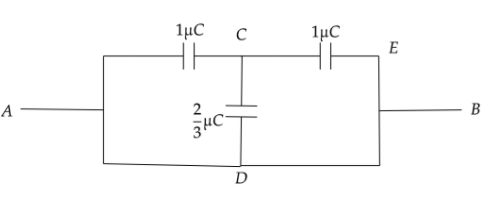
Now on solving the total capacitance of the branch DCE we will get,
Two capacitor $1\mu C$ and $\dfrac{2}{3}\mu C$ are connected parallel to each other hence,
${C_{DCE}} = {C_1} + {C_{\dfrac{2}{3}}}$
Where,
${C_{DCE}}$ is the total capacitance.
${C_1}$ and ${C_{\dfrac{2}{3}}}$ are conned in parallel, capacitance equal to $1\mu C$ and $\dfrac{2}{3}\mu C$ respectively.
Now putting the known values in the above equation we will get,
${C_{DCE}} = 1\mu C + \dfrac{2}{3}\mu C = \dfrac{5}{3}\mu C$
Now the circuit will look like,

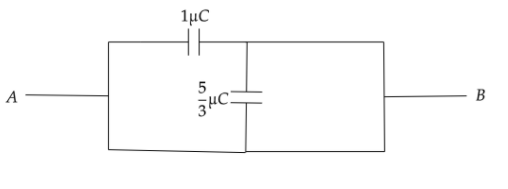
Now this two capacitor are in parallel to each other hence the total capacitance across AB is,
${C_{AB}} = {C_1} + {C_{\dfrac{5}{3}}}$
Where,
${C_{AB}}$ is the equivalent capacitance.
${C_1}$ and ${C_{\dfrac{5}{3}}}$ are conned in series capacitance equal to $1\mu C$ and $\dfrac{5}{3}\mu C$ respectively.
${C_{AB}} = 1\mu C + \dfrac{5}{3}\mu C = \dfrac{8}{3}\mu C$
Therefore the correct option is (B).

Note:
Remember that the total resistance of a circuit is calculated just opposite to the total capacitance. The formula used to find the total resistance in parallel is similar to the total capacitance in series and vice versa. Note that a capacitor is an electrical device that stores energy in the form of electrical charges.