Question

The equivalent capacitance between A and B is:

A. $1\;\mu F$
B. $2\;\mu F$
C. $1.5\;\mu F$
D. $3\;\mu F$

Answer 1

From the diagram, we see that the inclined capacitors are connected in series with each other whereas they are connected in parallel with the capacitor in the lower straight branch. To this end, determine the effective capacitance between the capacitors in series and consequently determine the equivalent capacitance between terminals A and B of the arrangement as an additive sum of individual capacitance.

Formula used:
Net capacitance in parallel $C_{net}= C_1+C_2$
Net capacitance in series $C_{series} = \dfrac{1}{C_1} + \dfrac{1}{C_2}$

Complete step-by-step answer:
We are given three capacitors that are connected across terminals A and B in a configuration as shown in the diagram.
$C_1 = C_2 = C_3 = 2\;\mu F$
We are now required to find the effective capacitance due to these three capacitors across A and B.

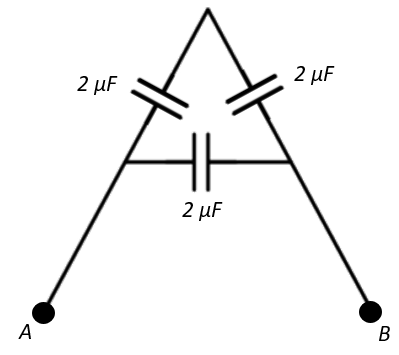
From the figure, we can see that $C_1$ and $C_2$ are connected in series with each other, whereas $C_3$ is connected in parallel with $C_1$ and $C_2$.
Therefore, we first calculate the effective capacitance of $C_1$ and $C_2$ that are in series with each other, i.e.,
$\dfrac{1}{C_{s}} = \dfrac{1}{C_1} + \dfrac{1}{C_2} = \dfrac{1}{2} + \dfrac{1}{2} = \dfrac{2+2}{4} = \dfrac{4}{4} = 1$
$\Rightarrow \dfrac{1}{C_{s}} = 1 \Rightarrow C_s = 1\;\mu F$
Now $C_3$ is in parallel with $C_s$, therefore, the equivalent capacitance between A and B will be:
$C_{eq} = C_3 +C_s = 2 + 1 = 3\;\mu F$

So, the correct answer is “Option D”.

Note: Remember that for capacitors in parallel, the net capacitance is the additive sum of individual capacitances, whereas for capacitors in parallel, the reciprocal of the net capacitance is the sum of the reciprocals of individual capacitances. The largest effective capacitance is obtained by connecting the capacitors in parallel, whereas the smallest effective capacitance is obtained by connecting the capacitors in series.
Do not get this confused with resistors, where for resistors in parallel, the reciprocal of the net resistance is the sum of the reciprocals of individual resistances resulting in the smallest effective resistance, whereas for resistors in series, the net resistance is the additive sum of individual resistances, resulting in the largest effective resistance.