Question
Question: The equivalent capacitance between A and B for the combination of capacitors shown in figure, where ...
The equivalent capacitance between A and B for the combination of capacitors shown in figure, where all capacitances are in microfarad is
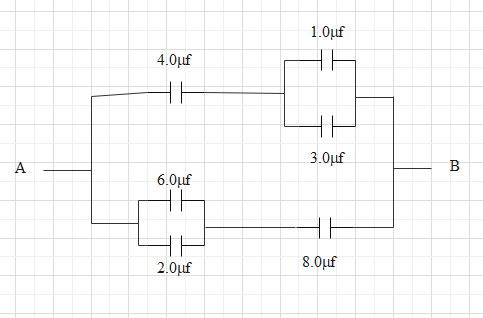
Solution
Hint: Express the mathematical formula to find the equivalent capacitance of more than one capacitor connected in series and parallel to each other. Simplify the circuit starting from the smallest loop and at last we will find our answer.
Complete step by step answer:
We can find the equivalent capacitance of more than one capacitor depending on the connection of the capacitors.
If two capacitors C1&C2 are connected in series than the equivalent capacitance C can be found out as,
C1=C11+C21
If two capacitors C1&C2 are connected in parallel than the equivalent capacitance will be,
C=C1+C2
Now, looking at the given circuit,
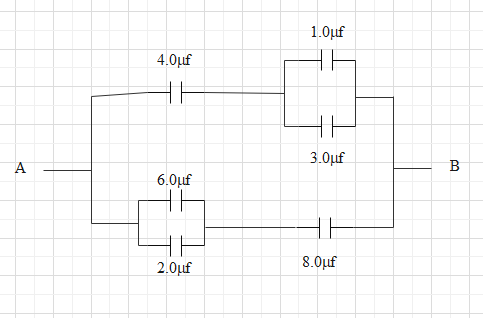
In the top part of the circuit we have a 1μF and one 3μF capacitor in parallel.
Let the equivalent capacitance will be C1
So,
C1=1μF+3μFC1=4μF
Again, at the bottom of the circuit we have one 6μF and one 2μF capacitor connected in parallel.
Let the equivalent capacitance is C2
So,
C2=6μF+2μFC2=8μF
So, the equivalent circuit becomes,
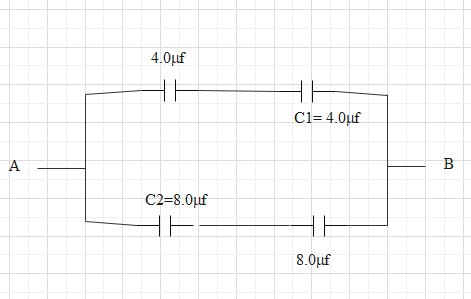
Now, at the top of the circuit we have one 4μF and one 4μF capacitor connected in series.
Let the equivalent capacitance is C3
So,
C31=4μF1+4μF1C31=4μF2C3=2μF
Again, at the bottom of the circuit we have one 8μF and one 8μF capacitor connected in series.
Let the equivalent capacitance is C4.
So,
C41=8μF1+8μF1C41=8μF2C4=4μF
So, the equivalent circuit becomes
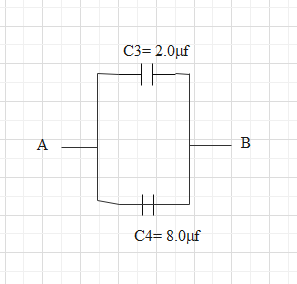
Now we have one 4μF and one 2μF capacitor in parallel. Let the equivalent capacitance is C.
So,
C=4μF+2μFC=6μF
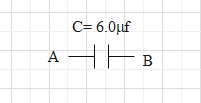
So, the equivalent capacitance of the circuit is 6μF.
Note: Capacitor is a device which stores electrical energy in presence of an electric field. Capacitors in series are the same as resistance in parallel while resistors in series are the same as capacitors in parallel.
