Question

The equivalent capacitance across $A$ and $B$ is:

A. $\dfrac{28}{3}\text{ }\mu \text{F}$
B. $\dfrac{15}{2}\text{ }\mu \text{F}$
C. $15\text{ }\mu \text{F}$
D. None of these

Answer 1

To find out the capacitance of the given circuit, the first step must be to simplify the circuit by drawing the capacitances that are in series or in parallel. The next step would be to find the equivalent capacitance of the circuit by simplifying the capacitances in series and in parallel. The last step would be to find the equivalent capacitance of the complete circuit.

Complete step-by-step answer:
Let us first draw a simplified circuit.

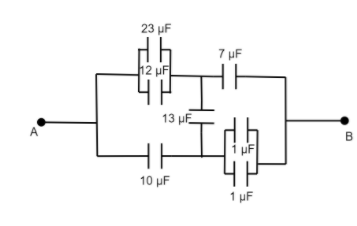
Now, the next step would be to find the equivalent capacitance of capacitors that are connected in parallel and capacitances that are connected in series. Equivalent capacitance of capacitors in series is as follows:
$\dfrac{1}{{{C}_{eq}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}$
Equivalent capacitance of capacitors in parallel is as follows:
${{C}_{eq}}={{C}_{1}}+{{C}_{2}}$
Now, let us further simplify the circuit by finding the equivalent capacitances:

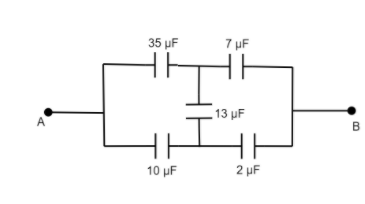
Since the ratio of:
$\dfrac{35}{10}=\dfrac{7}{2}$
Hence the $13\text{ }\mu \text{F}$ capacitor can be neglected. Now the circuit will look like:

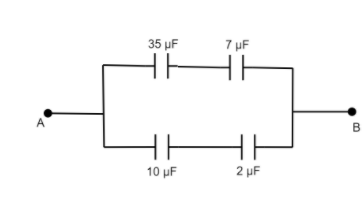
Now let us calculate the equivalent capacitance for the capacitors that are connected in series:

& \dfrac{1}{{{C}_{eq1}}}=\dfrac{1}{35}+\dfrac{1}{7} \\\ & \Rightarrow \dfrac{1}{{{C}_{eq1}}}=\dfrac{1+5}{35} \\\ & \Rightarrow \dfrac{1}{{{C}_{eq1}}}=\dfrac{6}{35} \\\ & \Rightarrow {{C}_{eq1}}=\dfrac{35}{6}\text{ }\mu \text{F} \\\ \end{aligned}$$ And, $$\begin{aligned} & \dfrac{1}{{{C}_{eq2}}}=\dfrac{1}{10}+\dfrac{1}{2} \\\ & \Rightarrow \dfrac{1}{{{C}_{eq2}}}=\dfrac{2+10}{20} \\\ & \Rightarrow \dfrac{1}{{{C}_{eq2}}}=\dfrac{12}{20} \\\ & \Rightarrow {{C}_{eq2}}=\dfrac{5}{3}\text{ }\mu \text{F} \\\ \end{aligned}$$ The circuit will now look like this now:  Again, we need to calculate the equivalent capacitance of the capacitors that are in parallel. The equivalent capacitance will be as follows: $\begin{aligned} & {{C}_{eq}}={{C}_{eq1}}+{{C}_{eq2}} \\\ & \Rightarrow {{C}_{eq}}=\dfrac{35}{6}+\dfrac{5}{3} \\\ & \Rightarrow {{C}_{eq}}=\dfrac{35+10}{6} \\\ & \Rightarrow {{C}_{eq}}=\dfrac{45}{6} \\\ & \therefore {{C}_{eq}}=\dfrac{15}{2}\text{ }\mu \text{F} \\\ \end{aligned}$ Thus, the correct option is $$B$$ because the equivalent capacitance across $A$ and $B$ is $\dfrac{15}{2}\text{ }\mu \text{F}$. **So, the correct answer is “Option B”.** **Note:** When the capacitances are in parallel, they are simply added to find out the equivalent capacitance of the given capacitors, but when they are connected in series then the inverse of the capacitors is used to find out the equivalent capacitance of the given capacitors.