Question

The equi-convex lens has a focal length$f$. If it is cut perpendicular to the principal axis passing through the optical centre, then the focal length of each half is.
$\begin{aligned} & \text{A}\text{.}\dfrac{f}{2} \\\ & \text{B}\text{. }f \\\ & \text{C}\text{.}\dfrac{3f}{2} \\\ & \text{D}.2f \\\ \end{aligned}$

Answer 1

Hint: Cutting an equi-convex lens through the optical centre and perpendicular to its principal axis, we will get the two halves as a plano-convex lens i.e. lens with one surface plane and other surface convex.

Formula used:
We know that the lens’ maker formula is given by the equation
$\dfrac{1}{f}=\left( n-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
Where,
$f$ is the focal length of lens
$n$ is the refractive index of material used
${{R}_{1}}$ is the radius of curvature of sphere 1
${{R}_{2}}$ is the radius of curvature of sphere 2.

Complete step-by-step answer:

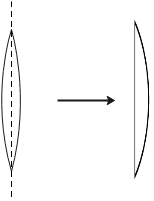
Assuming the direction of light along positive x-direction.
Now,
For equi-convex lens,
${{R}_{1}}=R,{{R}_{2}}=-R\And \text{focal length}=f$
So, from lens’ maker formula,
$\begin{aligned} & \dfrac{1}{f}=\left( n-1 \right)\left( \dfrac{1}{R}-\dfrac{1}{-R} \right)\Rightarrow \dfrac{1}{f}=\dfrac{2\left( n-1 \right)}{R} \\\ & \Rightarrow f=\dfrac{R}{2\left( n-1 \right)}\text{ }\cdots \cdots E{{q}^{n}}.\to \left( 1 \right) \\\ \end{aligned}$
For plano-convex lens,
${{R}_{1}}=R,{{R}_{2}}=\infty \And \text{ focal length}=f'$
So, from lens’ maker formula,
$\begin{aligned} & \dfrac{1}{f'}=\left( n-1 \right)\left( \dfrac{1}{R}-\dfrac{1}{\infty } \right)\Rightarrow \dfrac{1}{f'}=\dfrac{n-1}{R} \\\ & \Rightarrow f'=\dfrac{R}{n-1}\text{ }\cdots \cdots E{{q}^{n}}.\to \left( 2 \right) \\\ \end{aligned}$
Now, dividing $E{{q}^{n}}.\to \left( 2 \right)$ by$E{{q}^{n}}.\to \left( 1 \right)$, we get
$\dfrac{f'}{f}=\dfrac{\dfrac{R}{n-1}}{\dfrac{R}{2\left( n-1 \right)}}\Rightarrow \dfrac{f'}{f}=2\Rightarrow f'=2f$
So, the focal length of the equi-convex lens gets doubled when it is cut through the optical centre perpendicular to the principal axis.
Hence, the correct answer is $\left( \text{D} \right)$.

Additional information:
The optical centre of a lens is a point inside it through which a ray of light passes undeviated while the principal axis is an imaginary axis which passes through the optical centre and on this axis focal points are located.

Note: Students should notice here that the lens is cut perpendicular to its principal axis, then the focal length is doubled. If it is cut parallel to the principal axis then the focal length will remain unchanged because the curvature of both the surfaces will remain unchanged and thus from the lens’ maker formula, focal length is unaffected. Field of view for the lens will change in this case.