Question
Question: The equations of a common tangent(s) to the parabola \[y={{x}^{2}}\text{ and }y=-{{\left( x-2 \right...
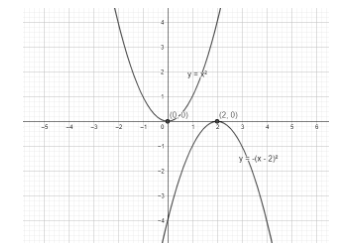
The equations of a common tangent(s) to the parabola y=x2 and y=−(x−2)2 is/ are:
This question has multiple correct options.
(a) y = 4 (x – 1)
(b) y = 0
(c) y = – 4 (x – 1)
(d) y = – 30x – 50
Solution
Hint : First assume the tangent of the curve in the slope intercept form. Now, substitute the equation of the line into the curve. Apply the condition of the line being tangent. Find the value of the constant in the equation of tangent in terms of the slope. Now, substitute this line in the second curve to derive the values of the slope, thus getting the constant. By this, you can get the equation of lines.
Complete step-by-step answer :
Given the equation of the curve for which we need to find the common tangent.
y=x2;y=−(x−2)2
Let us assume an equation of the line with variables as m, c, we get:
y = mx + c
Let this be the common tangent to the given curves. By this statement, we can say that the line is:
y = mx + c is the tangent to the curve y=x2.....(i)
y = mx + c is the tangent to the curve y=−(x−2)2.....(ii)
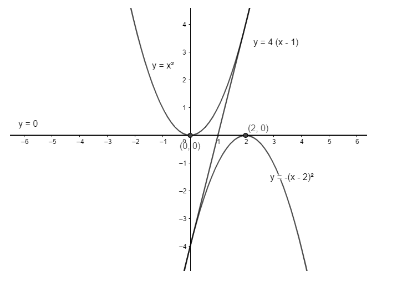
By statement (i), we can say that if we substitute the equation of the line into the curve, we must get only one point, because tangent only touches the curve. By substituting the equation of the line into the curve, we get it as:
mx+c=x2
By subtracting mx + c on both the sides, we can write it as:
x2−(mx+c)=(mx+c)−(mx+c)
x2−mx−c=0
So, for a quadratic to have one root, the condition is to have equal roots.
