Question
Question: The equation \(|z-1{{|}^{2}}+|z+1{{|}^{2}}=2\) represents A.A circle of radius one unit. B.A pai...
The equation ∣z−1∣2+∣z+1∣2=2 represents
A.A circle of radius one unit.
B.A pair of straight lines
C.The ordered pair (0,0)
D.Parabola
Solution
Hint: Focus on the point that the variable z in the above equation represents a general complex number, so we can consider z=x+iy and solve the equation. Remember that the argument of a complex number z=x+iy is equal to x2+y2 .
Complete step-by-step answer:
To start with the solution, we will let the complex number z be equal to x+iy, such that both x and y are real numbers.
Now if we put the assumed value of x in the equation given in the question, we get
∣z−1∣2+∣z+1∣2=2
⇒∣x+iy−1∣2+∣x+iy+1∣2=2
⇒∣x−1+iy∣2+∣x+1+iy∣2=2
Now we know that the argument of a complex number z=x+iy is equal to x2+y2 . So, using this formula in our equation, we get
((x−1)2+y2)2+((x+1)2+y2)2=2
⇒(x−1)2+y2+(x+1)2+y2=2
Now we will use the formula (a+b)2=a2+b2+2ab and (a−b)2=a2+b2−2ab .
x2+1−2x+y2+x2+1+2x+y2=2
⇒2x2+2y2=0
⇒x2+y2=0
We know that the sum of the squares of two real numbers is zero if and only if both the numbers are zero. So, we can say that the equation represents the point (0,0) as x and y both must be zero for the equation to be satisfied.
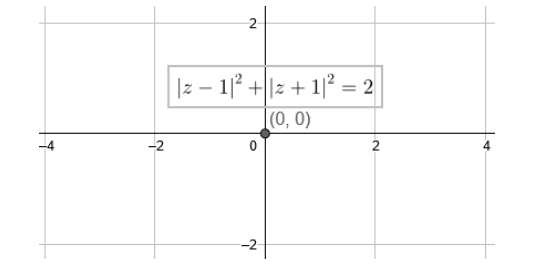
Therefore, the answer to the above question is option (c).
Note: Be careful with the signs and calculations as in such questions, the possibility of making a mistake is either of the sign or a calculation error. Also, don’t confuse between the signs of modulus and the argument, as both are represented using |z| sign.
