Question

The equation $\sin x + x \cos x = 0$ has atleast one root in the interval

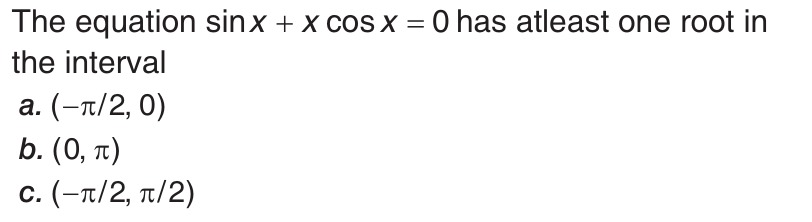
• A. (-\pi/2, 0)
• B. (0, \pi)
• C. (-\pi/2, \pi/2)

Answer 1

Answer: (B), (C)

(0, \pi), (-\pi/2, \pi/2)

Answer 2

Let $f(x) = \sin x + x \cos x$. We seek intervals containing roots of $f(x)=0$.

1. Check $x=0$: $f(0) = \sin 0 + 0 \cos 0 = 0$. So $x=0$ is a root.

2. Check options:

   a. $(-\pi/2, 0)$: Does not contain $0$. $f'(x) = 2 \cos x - x \sin x$. For $x \in (-\pi/2, 0)$, $f'(x) > 0$, so $f(x)$ is strictly increasing. Since $f(0)=0$, $f(x) < 0$ for $x \in (-\pi/2, 0)$. No root in $(-\pi/2, 0)$. b. $(0, \pi)$: Does not contain $0$. $f(0)=0$ and $f(\pi)=-\pi$. For small $\epsilon > 0$, $f(\epsilon) \approx 2\epsilon > 0$. Since $f(\epsilon)>0$ and $f(\pi)<0$, by IVT, there is a root in $(\epsilon, \pi) \subset (0, \pi)$. c. $(-\pi/2, \pi/2)$: Contains $0$. Since $x=0$ is a root, this interval contains a root.

Both options (b) and (c) contain at least one root.