Question

The equation of the tangents drawn from the origin to the circle${{x}^{2}}+{{y}^{2}}-2rx-2hy+{{h}^{2}}=0,$ are
(a) $x=0$
(b) $y=0$
(c) $\left( {{h}^{2}}-{{r}^{2}} \right)x-2rhy=0$
(d) $\left( {{h}^{2}}-{{r}^{2}} \right)x+2rhy=0$

Answer 1

Hint: The equation of a line passing through the origin can be assumed as y = mx where m is the slope of this line. Since this line is a tangent to the given circle i.e. ${{x}^{2}}+{{y}^{2}}-2rx-2hy+{{h}^{2}}=0$, we can apply the condition of tangency for a line to be the tangent of the circle from which, we will get an equation which can be solved to obtain the value of m.

Complete step by step answer:
It is given a circle ${{x}^{2}}+{{y}^{2}}-2rx-2hy+{{h}^{2}}=0..........(i)$
For a general circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+C=0$
Centre is $\left( -g,-f \right)$ and radius $=\sqrt{{{g}^{2}}+{{f}^{2}}-C}$
So, for the given circle in equation $\left( i \right)$, centre $\equiv \left( r,h \right)$ and radius
$\begin{aligned} & =\sqrt{{{r}^{2}}+{{h}^{2}}-{{h}^{2}}} \\\ & =\sqrt{{{r}^{2}}} \\\ & =r \\\ \end{aligned}$
Now, we can plot this circle using the above data 🡪

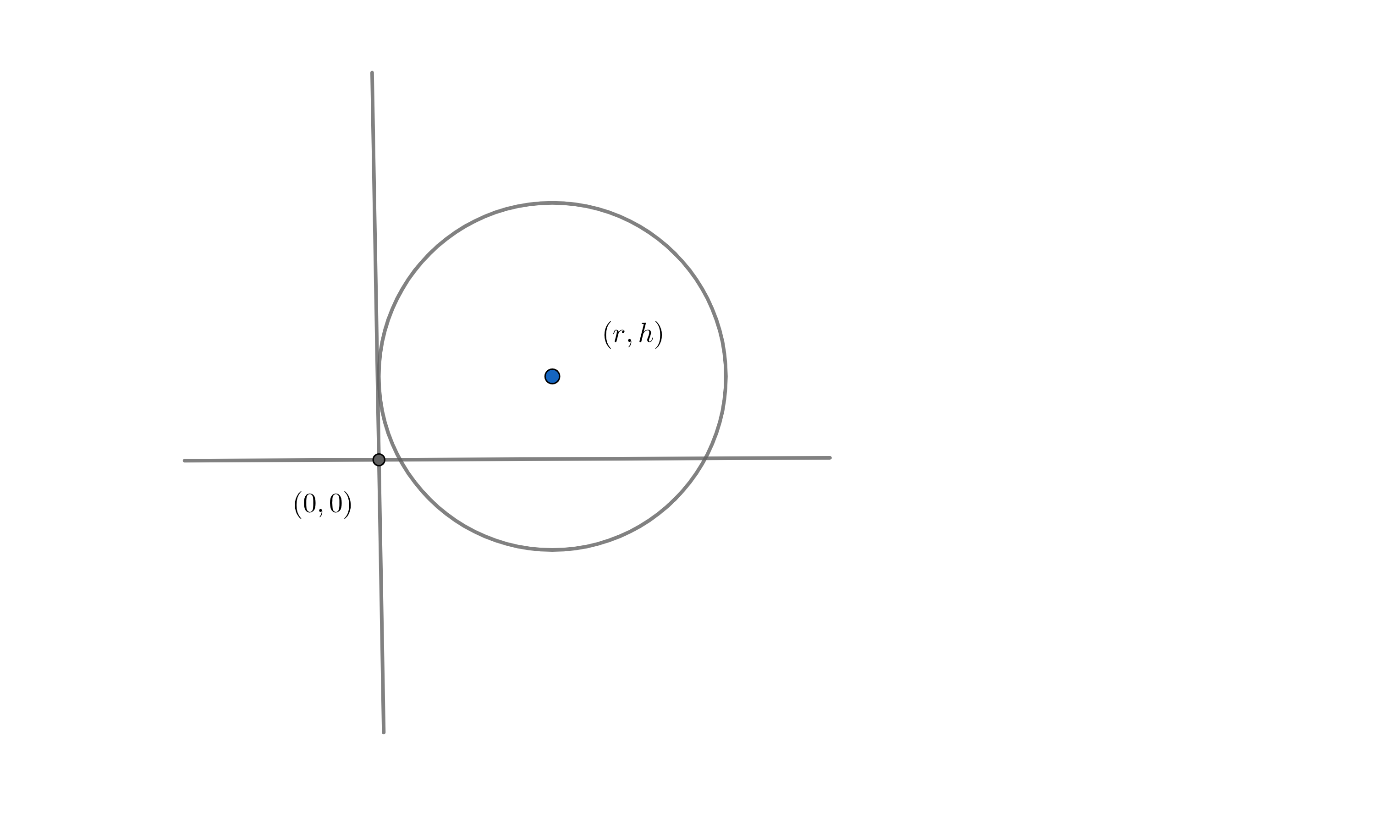
Since tangent is to be drawn from the origin, let the equation of the tangent be,
$y=mx..........(ii)$
We can see the above line has (0,0) on it.
Substituting tangent equation $\left( ii \right)$ in equation$\left( i \right)$, we get ,
${{x}^{2}}+{{\left( mx \right)}^{2}}-2rx-2h(mx)+{{h}^{2}}=0$
$\begin{aligned} & {{x}^{2}}+{{m}^{2}}{{x}^{2}}-2rx-2hmx+{{h}^{2}}=0 \\\ & \Rightarrow {{x}^{2}}+\left( {{m}^{2}}+1 \right)-2x\left( r+mh \right)+{{h}^{2}}=0...........(iii) \\\ \end{aligned}$
The above equation is a quadratic equation. For the equation $\left( ii \right)$ to be tangent, it must touch the circle at a single point. This means the above quadratic equation must have the same roots which is possible only when discriminant $\left( D \right)=0$.
For quadratic equation $a{{x}^{2}}+bx+C=0$
$D={{b}^{2}}-4ac$
From equation$\left( iii \right)$, substituting $a=\left( {{m}^{2}}+1 \right),\text{ }b\left( -2\left( r+mh \right) \right)\text{ and }C={{h}^{2}}$, we get,
$D={{\left( -2\left( r+mh \right) \right)}^{2}}-4{{h}^{2}}\left( {{m}^{2}}+1 \right)$
As explained int the above paragraph, discriminant $D=0$.

& \Rightarrow 4{{\left( r+mh \right)}^{2}}-4{{h}^{2}}\left( {{m}^{2}}+1 \right)=0 \\\ & \Rightarrow 4\left( {{r}^{2}}+{{m}^{2}}{{h}^{2}}+2rmh \right)-4{{h}^{2}}{{m}^{2}}-4{{h}^{2}}=0 \\\ & \Rightarrow 4{{r}^{2}}+4{{m}^{2}}{{h}^{2}}+8rmh-4{{m}^{2}}{{h}^{2}}-4{{h}^{2}}=0 \\\ & \Rightarrow 4{{r}^{2}}+8rmh-4{{h}^{2}}=0 \\\ & \Rightarrow {{r}^{2}}+2rmn-{{h}^{2}}=0 \\\ & \Rightarrow \left( 2rh \right)m={{h}^{2}}-{{r}^{2}} \\\ & \Rightarrow m=\dfrac{{{h}^{2}}-{{r}^{2}}}{2rh} \\\ \end{aligned}$$ Substituting this value of $m$in equation $\left( ii \right)$, Equation of tangent$\to y=\dfrac{\left( {{h}^{2}}-{{r}^{2}} \right)}{2hr}x$ $\Rightarrow \left( {{h}^{2}}-{{r}^{2}} \right)x-2hry=0$ If we observe carefully in the figure that we have drawn, we can see the circle is touching the $y$ - axis. So, $y$ - axis is also a tangent. So, another tangent is $x=0$ i.e. $y$- axis. The two tangents are, $x=0$ and $\left( {{h}^{2}}-{{r}^{2}} \right)x-2hry=0$ _So, Option (a) and Option (c)._ Note: There may be a possibility that one may not notice $x=0$ as the tangent. So, we should carefully observe the figure and this shows the importance of plotting the curve in a question.