Solveeit Logo
Login

Question

Question: The equation of the tangent to the circle \({x^2} + {y^2} = 25\) which is inclined at \({60^ \circ }...

The equation of the tangent to the circle x2+y2=25{x^2} + {y^2} = 25 which is inclined at 60∘{60^ \circ } angle with xx- axis, will be
A. y=3x±10y = \sqrt 3 x \pm 10
B. y=3x±2y = \sqrt 3 x \pm 2
C. 3y=x±10\sqrt 3 y = x \pm 10
D. None of these

Explanation

Solution

First, let the equation of the tangent is y=mx+cy = mx + c, where mm is the slope of the line. Also, the slope of the equation can be calculated using the given angle, which is tan⁡θ\tan \theta , when θ\theta is the angle inclined by xx axis. Then, substitute the value of yy in the equation of the circle, x2+y2=25{x^2} + {y^2} = 25 to form a quadratic equation. Next, solve for ccby putting the discriminant of the equation to zero.

Complete step-by-step answer:
We have to find the equation of the tangent to the circle x2+y2=25{x^2} + {y^2} = 25 and we are given that the tangent is inclined at 60∘{60^ \circ } with xx axis.
Let the equation of the tangent be y=mx+cy = mx + c, where mm is the slope of the line.
We also know that the slope of the line which is inclined at angle θ\theta with the xx axis is tan⁡θ\tan \theta .

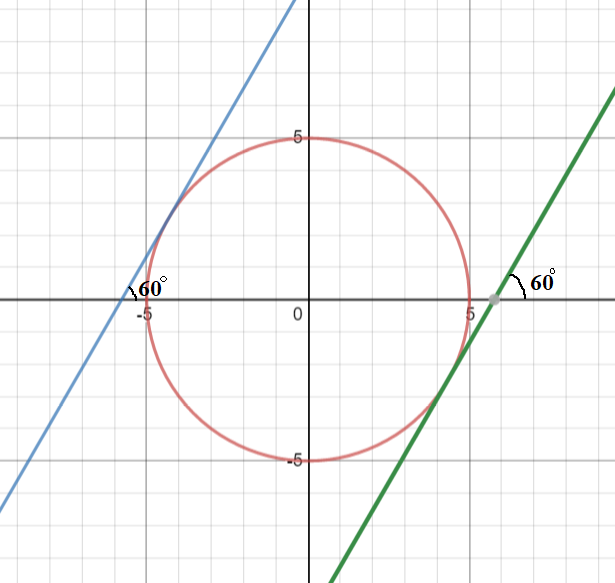
Here, the tangent is inclined at 60∘{60^ \circ } with xx axis, therefore the slope of the tangent is tan⁡60∘\tan {60^ \circ } which is equal to 3\sqrt 3
Then, the equation of tangent is y=3x+cy = \sqrt 3 x + c
Now, we will substitute the value of y=3x+cy = \sqrt 3 x + c in the equation of circle, x2+y2=25{x^2} + {y^2} = 25.
x2+(3x+c)2=25 ⇒x2+3x2+c2+23cx=25 ⇒4x2+23cx+c2−25=0  {x^2} + {\left( {\sqrt 3 x + c} \right)^2} = 25 \\\ \Rightarrow {x^2} + 3{x^2} + {c^2} + 2\sqrt 3 cx = 25 \\\ \Rightarrow 4{x^2} + 2\sqrt 3 cx + {c^2} - 25 = 0 \\\
Also, for the equation of the tangent , the discriminant of the equation should be zero.
If ax2+bx+c=0a{x^2} + bx + c = 0 is the equation, then the discriminant is given as D=b2−4acD = {b^2} - 4ac
Then,
(23c)2−4(4)(c2−25)=0 ⇒12c2−16(c2−25)=0 ⇒12c2−16c2+400=0 ⇒4c2=400  {\left( {2\sqrt 3 c} \right)^2} - 4\left( 4 \right)\left( {{c^2} - 25} \right) = 0 \\\ \Rightarrow 12{c^2} - 16\left( {{c^2} - 25} \right) = 0 \\\ \Rightarrow 12{c^2} - 16{c^2} + 400 = 0 \\\ \Rightarrow 4{c^2} = 400 \\\
On dividing the equation by 4, we will get,
c2=100 ⇒c=±10  {c^2} = 100 \\\ \Rightarrow c = \pm 10 \\\
We will substitute the value of the c=±10c = \pm 10 in the equation of the tangent,
y=3x±10y = \sqrt 3 x \pm 10
Hence, option A is correct.

Note: If the discriminant is zero, then the line is tangent to the curve. If the discriminant is greater than 0, then the line intersects the curve at two points and if the discriminant is less than 0, then the line does not intersect the curve.