Question
Question: The equation of the plane containing the line $\frac{x+1}{-3}=\frac{y-3}{2}=\frac{z+2}{1}$ and the p...
The equation of the plane containing the line −3x+1=2y−3=1z+2 and the point (0, 7, -7) is
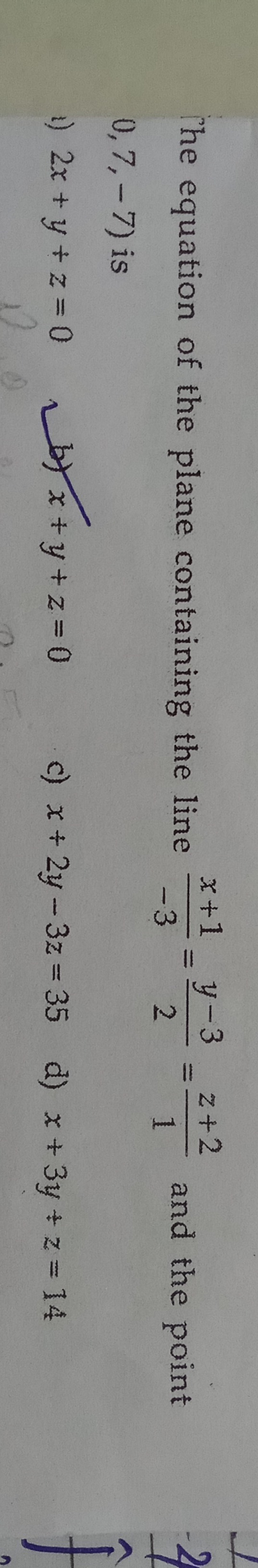
2x + y + z = 0
x + y + z = 0
x + 2y - 3z = 35
x + 3y + z = 14
x + y + z = 0
Solution
To find the equation of the plane, we can follow these steps:
-
Find a point on the line and its direction vector:
The given line is −3x+1=2y−3=1z+2. A point on this line is Q(−1,3,−2), and the direction vector is d=(−3,2,1).
-
Find another vector in the plane:
We are given the point P(0,7,−7). The vector from Q to P is QP=P−Q=(0−(−1),7−3,−7−(−2))=(1,4,−5).
-
Find the normal vector to the plane:
The normal vector n is the cross product of d and QP: n=d×QP=(−3,2,1)×(1,4,−5).
Calculating the cross product: n=(2(−5)−1(4),−((−3)(−5)−1(1)),−3(4)−2(1))=(−10−4,−(15−1),−12−2)=(−14,−14,−14).
We can simplify this normal vector by dividing by -14 to get n=(1,1,1).
-
Write the equation of the plane:
Using the point-normal form of the equation of a plane, we have: 1(x−0)+1(y−7)+1(z+7)=0, which simplifies to x+y−7+z+7=0, and further simplifies to x+y+z=0.
Therefore, the equation of the plane is x+y+z=0.
