Question

The equation of the plane bisecting the angle between the planes 3x+4y = 4 and 6x-2y+3z+5=0 containing the origin is
[a] 9x-38y+15z+43=0
[b] 51x+18y+15z=3
[c] 9x+2y+3z+1=0
[d] 17x+9y+15z=26

Answer 1

Use the fact that the angle between two planes is the angle between their normal. Hence if a plane bisects the angle between the planes, then the normal vector of the bisector plane must be in plane with the normal vectors of the other two planes and make equal angles with them. Use the theorem in the plane, i.e. if $\overrightarrow{a}$ and $\overrightarrow{b}$ are two non-collinear vectors in a plane, then every vector in that plane is a linear combination of the vectors if $\overrightarrow{a}$ and $\overrightarrow{b}$. Use the fact that the angle between two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ is given by $\cos \theta =\dfrac{\overrightarrow{a}\cdot \overrightarrow{b}}{\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|}$. Hence find the normal vector of the bisector plane and hence find the equation of the plane.

Complete step-by-step solution:
__
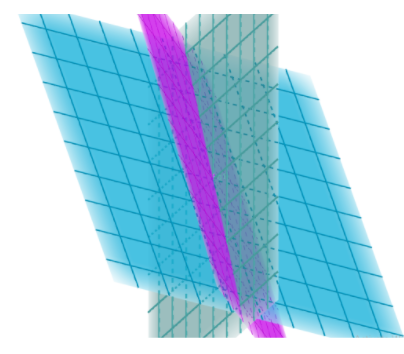
The grey plane is the plane 3x+4y = 4 and the blue plane is the plane 6x-2y+3z+5 = 0.
The purple plane is the bisector plane of the angle containing the origin.

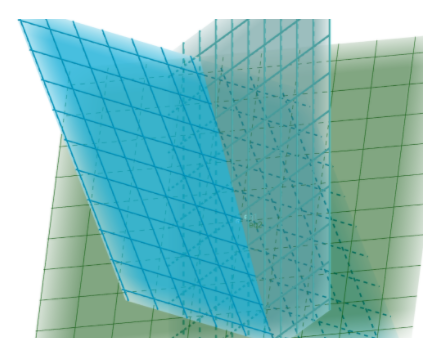
The green plane is the bisector plane of the angle not containing the origin
We know that the normal vector of the plane $ax+by+cz=d$ is given by $\overrightarrow{n}=a\widehat{i}+b\widehat{j}+c\widehat{k}$
Hence, we have
The normal vector of the plane $3x+4y=4$ is given by $\overrightarrow{n}=3\widehat{i}+4\widehat{j}$
Again, we have
The normal vector of the plane $6x-2y+3z+5=0$ is given by $\overrightarrow{m}=6\widehat{i}-2\widehat{j}+3\widehat{k}$
We know that the angle between two planes is the angle between their normal. Hence if a plane bisects the angle between the planes, then the normal vector of the bisector plane must be in plane with the normal vectors of the other two planes and make equal angles with them.
Let the normal vector of the bisector plane by $\overrightarrow{v}$.
Hence by theorem in the plane, we have
$\overrightarrow{v}=\lambda \overrightarrow{m}+\mu \overrightarrow{n}=\left( 6\lambda +3\mu \right)\widehat{i}+\left( -2\lambda +4\mu \right)\widehat{j}+3\lambda \widehat{k}$
Now, since $\overrightarrow{v}$ is the normal vector of the bisector plane, we have
$\begin{aligned} & \left| \dfrac{m\cdot v}{\left| m \right|\left| v \right|} \right|=\left| \dfrac{n\cdot v}{\left| n \right|\left| v \right|} \right| \\\ & \Rightarrow \left| \dfrac{m\cdot v}{\left| m \right|} \right|=\left| \dfrac{n\cdot v}{\left| n \right|} \right| \\\ \end{aligned}$
Hence, we have

& \left| \dfrac{6\left( 6\lambda +3\mu \right)-2\left( -2\lambda +4\mu \right)+3\left( 3\lambda \right)}{\sqrt{{{6}^{2}}+{{2}^{2}}+{{3}^{2}}}} \right|=\left| \dfrac{3\left( 6\lambda +3\mu \right)+4\left( -2\lambda +4\mu \right)}{\sqrt{{{3}^{2}}+{{4}^{2}}}} \right| \\\ & \Rightarrow \left| \dfrac{36\lambda +18\mu +4\lambda -8\mu +9\lambda }{7} \right|=\left| \dfrac{18\lambda +9\mu -8\lambda +16\mu }{5} \right| \\\ & \Rightarrow \left| \dfrac{49\lambda +10\mu }{7} \right|=\left| \dfrac{10\lambda +25\mu }{5} \right| \\\ & \Rightarrow \dfrac{49\lambda +10\mu }{7}=\pm \dfrac{10\lambda +25\mu }{5} \\\ \end{aligned}$$ Taking the positive sign, we get $$\dfrac{49\lambda +10\mu }{7}=\dfrac{10\lambda +25\mu }{5}$$ Cross-multiplying, we get $\begin{aligned} & 245\lambda +50\mu =70\lambda +175\mu \\\ & \Rightarrow 175\lambda =125\mu \\\ & \Rightarrow \lambda =\dfrac{125}{175}\mu =\dfrac{5}{7}\mu \\\ \end{aligned}$ Taking $\mu =7$, we get $\lambda =5$ Hence, we have $\overrightarrow{v}=51\widehat{i}+18\widehat{j}+15\widehat{k}=3\left( 17\widehat{i}+6\widehat{j}+5\widehat{k} \right)$ We know that if $\overrightarrow{v}$ is the normal vector, then so is $$k\overrightarrow{v}$$, where k is any scalar. Hence, we have $\dfrac{\overrightarrow{v}}{3}=17\widehat{i}+6\widehat{j}+5\widehat{k}$ is the normal vector of a bisector plane. Taking the negative sign and cross multiplying, we get $\begin{aligned} & 245\lambda +50\mu =-70\lambda -175\mu \\\ & \Rightarrow 315\lambda =-225\mu \\\ & \Rightarrow \lambda =-\dfrac{5}{7}\mu \\\ \end{aligned}$ Taking $\mu =7$, we get $\lambda =5$ Hence, we have $\overrightarrow{v}=-9\widehat{i}+38\widehat{j}-15\widehat{k}$ Finding a common point on the planes: We take z = 0 Hence the equations of the two planes become $\begin{aligned} & 3x+4y=4\text{ }\left( i \right) \\\ & 6x-2y=-5\text{ }\left( ii \right) \\\ \end{aligned}$ Multiplying equation (ii) by 2 and adding the two equations, we get $\begin{aligned} & 15x=-6 \\\ & \Rightarrow x=\dfrac{-2}{5} \\\ \end{aligned}$ Substituting the value of x in equation (ii), we get $\begin{aligned} & \dfrac{-12}{5}-2y=-5 \\\ & \Rightarrow 2y=\dfrac{13}{5} \\\ & \Rightarrow y=\dfrac{13}{10} \\\ \end{aligned}$ Hence the point common on the planes is $\left( \dfrac{-2}{5},\dfrac{13}{10},0 \right)$ The bisector planes also should pass through this point. Hence, we have The equation of one bisector plane is $\begin{aligned} & 17\left( x+\dfrac{2}{5} \right)+6\left( y-\dfrac{13}{10} \right)+5z=0 \\\ & \Rightarrow 170x+68+60y-78+50z=0 \\\ & \Rightarrow 170x+60y+50z-10=0 \\\ & \Rightarrow 17x+6y+5z-1=0 \\\ \end{aligned}$ The equation of the other bisector plane is $\begin{aligned} & -9\left( x+\dfrac{2}{5} \right)+38\left( y-\dfrac{13}{10} \right)-15z=0 \\\ & \Rightarrow -90x-36+380y-494-150z=0 \\\ & \Rightarrow -90x+380y-150z-530=0 \\\ & \Rightarrow -9x+38y-15z-53=0 \\\ & \Rightarrow 9x-38y+15z+53=0 \\\ \end{aligned}$ Consider the plane $17x+6y+5z-1 = 0$ Substitituting $x = y =z = 0$, we have LHS = $-1$ For plane $9x-38y+15z+53 = 0$, substituting $x=0=y=z$, we have LHS =$ 53$ For plane $3x+4y-4 = 0$ substituting $x= y = z =0$, we have LHS = $-4$ For plane $6x-2y+3z+5 =0$, substituting $x= y = z =0$, we have LHS =$ 5$ Hence, we have origin is above plane $6x-2y+3z+5 =0$ and below plane $ 3x+4y-4 = 0$. Also, we have distance of $(0,0,0)$ from $6x-2y+3z+5=0$ $=\dfrac{5}{\sqrt{{{6}^{2}}+{{2}^{2}}+{{3}^{2}}}}=\dfrac{5}{7}$ and the distance of $(0,0,0) $ from $3x+4y-4$ is $\dfrac{4}{\sqrt{{{3}^{2}}+{{4}^{2}}}}=\dfrac{4}{5}$ Since $\dfrac{4}{5}>\dfrac{5}{7}$, we have for the plane bisecting the origin containing angle, the origin should be on the same side as that of $3x+4y-4 =0$, which is $17x+6y+5z-1 = 0$, which is the same as an option [b] (Divide by 3 on both sides) **Hence option [b] is correct.** **Note:** Alternatively, we can use the fact that the equation of the planes bisecting the angle between the plane ${{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}z+{{d}_{1}}=0$ and ${{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}z+{{d}_{2}}=0$ is given by $\dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}z+{{d}_{1}}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}}=\pm \dfrac{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}z+{{d}_{2}}}{\sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}$. Using this property, we can directly find the equation of the planes and hence determine the bisector containing the origin.