Question
Question: The equation of the perpendicular bisector of the line segment joining \(A\left( {2,3} \right)\) and...
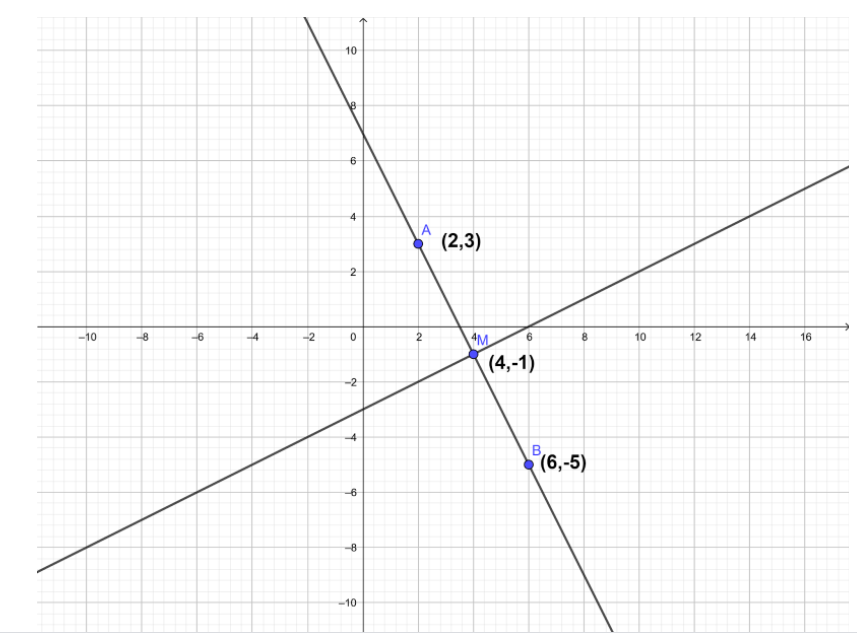
The equation of the perpendicular bisector of the line segment joining A(2,3) and B(6,−5) is:
(A) x−y=−1
(B) x−2y=3
(C) x+y=3
(D) x−2y=6
Solution
Hint : In the given problem, we are required to find the equation of the perpendicular bisector of the line formed by the join of the given two points. We first find the slope of the line formed by joining the given points. Then, we find the slope of the required line. We will find out the midpoint of the two given points using the midpoint formula and then use the slope point to form a straight line in order to get to the equation of the required line.
Complete step-by-step answer :
So, we are given the points A(2,3) and B(6,−5). Now, by joining these two points, we get a line whose slope can be calculated using the formula (x2−x1y2−y1).
Let us consider x1=2, y1=3, x2=6 and y2=−5.
So, we get the slope of the line as (6−2−5−3)=4−8=−2.
So, we get the slope of the line formed by joining these two points A(2,3) and B(6,−5) as −2.
Now, we know that the perpendicular bisector is a line that is perpendicular to the given line and passes through the midpoint of the line joining the two given points.
We also know that the product of the slopes of two perpendicular lines is always −1. Since the slope of the line formed by joining the two given points is −2, so the slope of the perpendicular bisector is 21 because (−2)×(21)=−1.
Now, we find the midpoint of the line joining the two endpoints A(2,3) and B(6,−5) using the midpoint formula (2x1+x2,2y1+y2).
So, we get the midpoint as M=(2x1+x2,2y1+y2).
Now, substituting the values of coordinates of the endpoint, we get,
⇒M=(22+6,23+(−5))
Now, simplifying the expression and carrying out the calculations, we get,
⇒M=(4,−1)
So, we get the slope of the required line as 21 and the coordinates of the point lying on the line as (4,−1).
We know the slope point form of the line, where we can find the equation of a straight line given the slope of the line and the point lying on it. The slope point form of the line can be represented as: (y−y3)=m(x−x3) where (x1,y1) is the point lying on the line given to us and m is the slope of the required straight line.
Consider x3=4and y3=−1 as the midpoint is (4,−1).
Therefore, required equation of line is as follows:
(y−(−1))=21(x−4)
On opening the brackets and simplifying further, we get,
⇒y+1=2x−4
Now, cross multiplying the terms of the equation, we get,
⇒2y+2=x−4
Taking all the variables to the left side of the equation and all constant on right side of equation, we get,
⇒2+4=x−2y
Simplifying the equation, we get,
⇒x−2y=6
Hence, the equation of the required straight line is: x−2y=6. So, option (D) is the correct answer.
Note : The given problem requires us to have thorough knowledge of the concepts of coordinate geometry. We must know the midpoint formula for solving the given question. We should remember the slope point form of a straight line to get the required answer. One must know that the product of the slopes of two perpendicular lines is one.
