Question

The equation of the parabola, whose vertex is $\left( { - 1, - 2} \right)$ axis is vertical and which passes through the point $\left( {3,6} \right)$ is
A. ${x^2} + 2x - 2y - 3 = 0$
B. $2{x^2} = 3y$
C. ${x^2} - 2x + y + 3 = 0$
D. None of these

Answer 1

Here in this question, we have to find the equation of the parabola of a given vertex. Given the parabola axis is vertical for vertical axis the equation of parabola at the origin is ${x^2} = 4ay$ or at any vertex $\left( {h,k} \right)$ the equation of parabola is ${\left( {x - h} \right)^2} = 4a\left( {y - k} \right)$, where a be a value that can be find by using a point $\left( {3,6} \right)$ and on further simplification we get the required solution.

Complete step by step answer:
A parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped.Consider the question: given the vertex of the parabola, whose axis is vertical and which passes through the point $\left( {3,6} \right)$. We have to find the equation of parabola? Since the given axis of the parabola is vertical, the equation of the parabola would be the form of ${x^2} = 4ay$.

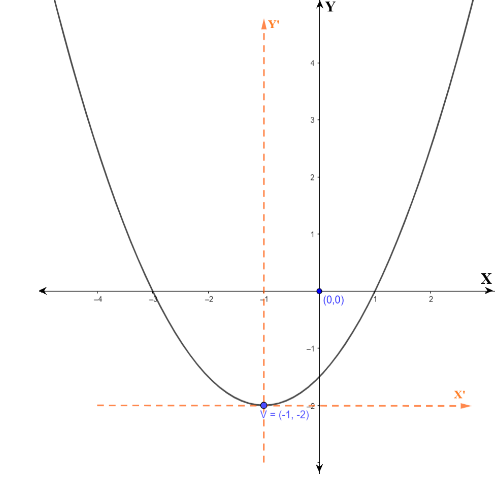
At any vertex $\left( {h,k} \right)$ the equation will be ${\left( {x - h} \right)^2} = 4a\left( {y - k} \right)$, then
The given vertex is $\left( { - 1, - 2} \right)$ the equation will be
$\Rightarrow \,\,{\left( {x - \left( { - 1} \right)} \right)^2} = 4a\left( {y - \left( { - 2} \right)} \right)$
On using sign convention, we have
$\Rightarrow \,\,{\left( {x + 1} \right)^2} = 4a\left( {y + 2} \right)$-----(1)

Now find the value of ‘a’. Given the parabola passes through the point $\left( {3,6} \right)$.
Substitute $x = 3$ and $y = 6$ value in equation (1), then we have
$\Rightarrow \,\,{\left( {3 + 1} \right)^2} = 4a\left( {6 + 2} \right)$
$\Rightarrow \,\,{4^2} = 4a\left( 8 \right)$
$\Rightarrow \,\,16 = 32a$
$\Rightarrow \,\,32a = 16$
Divide both side by 32
$\Rightarrow \,\,a = \dfrac{{16}}{{32}}$
Divide both numerator and denominator by 16, then we get
$\therefore \,\,a = \dfrac{1}{2}$

Substitute the value of a in equation (1), then
$\Rightarrow \,\,{\left( {x + 1} \right)^2} = 4\left( {\dfrac{1}{2}} \right)\left( {y + 2} \right)$
On simplification, we have
$\Rightarrow \,\,{\left( {x + 1} \right)^2} = 2\left( {y + 2} \right)$
Apply a algebraic identity: ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$, then
$\Rightarrow \,\,{x^2} + {1^2} + 2\left( x \right)\left( 1 \right) = 2y + 4$
$\Rightarrow \,\,{x^2} + {1^2} + 2x = 2y + 4$
Subtract $\left( {2y + 4} \right)$ on both side, we have
$\Rightarrow \,\,{x^2} + 1 + 2x - \left( {2y + 4} \right) = 2y + 4 - \left( {2y + 4} \right)$
$\Rightarrow \,\,{x^2} + 1 + 2x - 2y - 4 = 2y + 4 - 2y - 4$
$\Rightarrow \,\,{x^2} + 1 + 2x - 2y - 4 = 0$
On simplification, we get
$\therefore \,\,{x^2} + 2x - 2y - 3 = 0$
Hence, the equation of parabola is ${x^2} + 2x - 2y - 3 = 0$.

Therefore, option A is correct.

Note: There are two general standard equation of a parabola having vertex $\left( {0,0} \right)$ is: if parabola is parallel to the y-axis or horizontal to the axis the standard equation of a parabola is ${y^2} = 4ax$similarly if parabola is parallel to the y-axis or vertical to the axis the standard equation of a parabola is ${x^2} = 4ay$.