Question

The equation of the line making an angle of $60{}^\circ$ with the x-axis and y-intercept $\dfrac{-2}{5}$ is

Answer 1

The angle made by the straight line is $60{}^\circ$ with the x-axis and its y-intercept is $\dfrac{-2}{5}$ . We know that slope is the tangent of the angle made by the straight line with the x-axis. Use $\tan 60{}^\circ =\sqrt{3}$ and get the slope of the straight line. We know the standard equation of a straight line, $y=mx+c$ , where, m is the slope of the straight line and c is its y-intercept. Now, solve it further and get the equation of the straight line.

Complete step by step answer:
According to the question, we are given that a straight line is making an angle of $60{}^\circ$ with the x-axis and the y-intercept of this line is equal to $\dfrac{-2}{5}$ .
The angle made by the straight line with the x-axis = $60{}^\circ$ ………………………………………….(1)
The y-intercept of the straight line = $\dfrac{-2}{5}$ ………………………………………………(2)
We know the standard equation of a straight line, $y=mx+c$ , where, m is the slope of the straight line and c is its y-intercept …………………………………………….(3)
We know that the property that the slope is the tangent of the angle made by the straight line with the x-axis ……………………………………(4)
Now, from equation (1) and equation (4), we get
Slope = $\tan 60{}^\circ$ ………………………………………..(5)
We also know that, $\tan 60{}^\circ =\sqrt{3}$ …………………………………………….(6)
Now, using equation (6) and on replacing $\tan 60{}^\circ$ by $\sqrt{3}$ in equation (5), we get
Slope = $\sqrt{3}$ …………………………………………(7)
Now, from equation (2), equation (3), and equation (7), we get
$\Rightarrow y=\sqrt{3}x+\left( -\dfrac{2}{5} \right)$
$\Rightarrow 5y=5\sqrt{3}x-2$ ……………………………………………………(8)
From equation (8), we have the equation of the straight line.

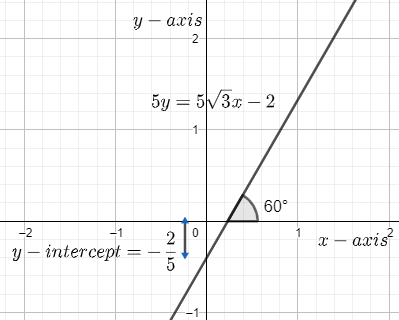
Therefore, the equation of the straight line is $5y=5\sqrt{3}x-2$.

Note: In this question, one might make a silly mistake and take $60{}^\circ$ as the angle made by the straight line with the negative x-axis. If we do so, then our slope will be equal to $-\sqrt{3}$ . This may prove wrong sometimes. So, when nothing is mentioned in the question, always try to use the angle given as the angle made by the straight line with the positive x-axis.