Question

The equation of the latus rectum of the hyperbola $\dfrac{{{\left( x-4 \right)}^{2}}}{16}-\dfrac{{{\left( y-3 \right)}^{2}}}{20}=1$ are
A. $x=1\pm 5$
B. $x=4\pm 6$
C. $x=2\pm 6$
D. $x=3\pm 5$

Answer 1

We first explain the mathematical aspect of the conic curve hyperbola. We find the general formula and explain different components of the curve. Then we discuss about the given conic curve $\dfrac{{{\left( x-4 \right)}^{2}}}{16}-\dfrac{{{\left( y-3 \right)}^{2}}}{20}=1$. For general equation of $\dfrac{{{\left( x-\alpha \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-\beta \right)}^{2}}}{{{b}^{2}}}=1$, the lines of latus recta are $x=\alpha \pm \sqrt{{{a}^{2}}+{{b}^{2}}}$. We put the values from $\dfrac{{{\left( x-4 \right)}^{2}}}{16}-\dfrac{{{\left( y-3 \right)}^{2}}}{20}=1$ to find the solution.

Complete step by step solution:
A hyperbola is the mathematical shape in the form of smooth curve formed by the intersection of two circular cones. The properties of hyperbola allow it to play an important role in the real world where designs and predictions of phenomena are heavily influenced by it.
The general equation hyperbola is $\dfrac{{{\left( x-\alpha \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-\beta \right)}^{2}}}{{{b}^{2}}}=1$.
For the general equation $\left( \alpha ,\beta \right)$ is the centre. The vertices are $\left( \alpha \pm a,\beta \right)$. The coordinates of the foci are $\left( \alpha \pm ae,\beta \right)$. Here $e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ is the eccentricity. The equations of the latus recta are $x=\alpha \pm ae=\alpha \pm \sqrt{{{a}^{2}}+{{b}^{2}}}$.
Now we talk about this conic curve of hyperbola $\dfrac{{{\left( x-4 \right)}^{2}}}{16}-\dfrac{{{\left( y-3 \right)}^{2}}}{20}=1$.

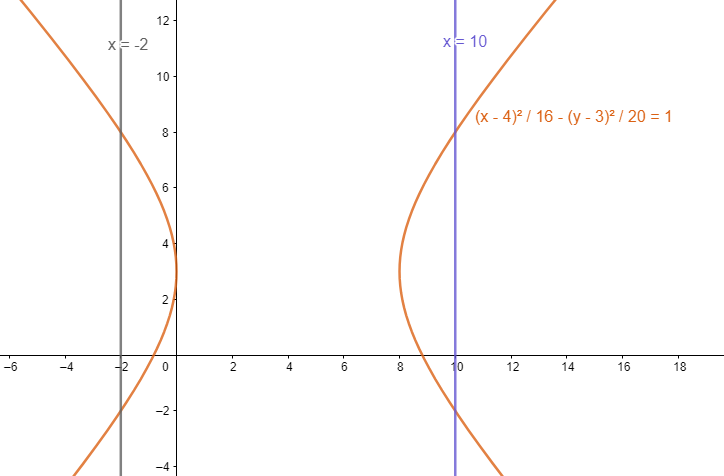
We equate it with the general formula and get $\alpha =4,{{a}^{2}}=16,{{b}^{2}}=20$.
So, the equations of the latus recta are $x=4\pm \sqrt{16+20}=4\pm 6$. The correct option is B.

Note: The hyperbola has an important mathematical equation associated with it - the inverse relation. When an increase in one trait leads to a decrease in another or vice versa which helps in explaining the relationship between the pressure and volume of a gas.