Question

The equation of the image of the pair of rays $y = \left| x \right|$ by the line $x = 1$ is
A) $\left| y \right| = x + 2$
B) $\left| y \right| + 2 = x$
C) $y = \left| {x - 2} \right|$
D) None of these

Answer 1

First we will find the intersection of both lines and then its image in the mirror. Then we will find the point of intersection of line and mirror, as the image of the line will also pass that point. Now, for each image of the line, we have 2 points, it will pass through. Thus, we will find the equation of the image of the line by using a two-point formula.

Complete step by step solution:

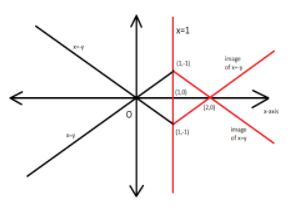
The given lines whose image is to be found are: $y = \left| x \right|$
So, the two lines are $y = x$ and $y = - x$
Equation of mirror is: $x = 1$
Now, Intersection of $y = x$ and $y = - x$
To find the intersection of above two lines, let the point of intersection is$\left( {a,b} \right)$, the point of intersection will lie on both the lines as per the definition of the intersection point.
Thus, substituting $\left( {a,b} \right)$in first line, we have
$b = a$ …(i)
Now, substituting $\left( {a,b} \right)$in second curve, we have
$b = - a$ …(ii)
Substituting (i) in (ii)
$a = - a \\\ 2a = 0 \\\ a = 0 \\\$
$b = a = 0$
So, $\left( {0,0} \right)$ is the point of intersection of $y = x$ and $y = - x$
Now, we will find the point where $y = x$ and $y = - x$intersects the mirror line, $x = 1$
For, $y = x$and $x = 1$, we can see the point of intersection is $\left( {1,1} \right)$
For, $y = - x$and $x = 1$, we can see the point of intersection is $\left( {1, - 1} \right)$
Now, the image of line $y = x$in the mirror $x = 1$will pass through $\left( {1,1} \right)$and image of point intersection of $y = x$ and $y = - x$ on the line $x = 1$
So, Image of point intersection of $y = x$ and $y = - x$ i.e. $\left( {0,0} \right)$on the line $x = 1$is $\left( {2,0} \right)$
Thus, image of both lines will pass through $\left( {2,0} \right)$
Now, equation of a line passing through two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$is:
$y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$
Thus, image of line $y = x$in the mirror $x = 1$will pass through $\left( {1,1} \right)$and $\left( {2,0} \right)$
Equation of required line: $y - 1 = \dfrac{{0 - 1}}{{2 - 1}}\left( {x - 1} \right)$
$y - 1 = - 1\left( {x - 1} \right)$
$x + y = 2$
$y = 2 - x$ …(iii)
And, image of line $y = - x$in the mirror $x = 1$will pass through $\left( {1, - 1} \right)$and $\left( {2,0} \right)$
Equation of required line: $y + 1 = \dfrac{{0 + 1}}{{2 - 1}}\left( {x - 1} \right)$
$y + 1 = \left( {x - 1} \right)$
$y = x - 2$ …(iv)
Thus, from (iii) and (iv), we have equation of images of lines as
$y = 2 - x$ and $y = x - 2$
Hence, combined equation is $y = \left| {x - 2} \right|$, so option C is correct.

Note: A different approach to the question can be taking any two random points on each line. For these two points, corresponding to a line, we will find their images in the mirror. Now, we know the image of the line will pass through the image of points. Thus, we have 2 points, we can find the equation of image by using the two-point formula.