Question

The equation of the ellipse with area $\frac{3P}{2}$ passing through the point of intersection of $x^2 + 4y^2 = 4$ and $x-1=0$, having x-axis as its major axis and eccentricity equal to $\frac{\sqrt{3}}{2}$, is $ax^2 + 2hxy + by^2 + 2gx + 2fy - 2 = 0$. There are same expressions given in the list - I whose values are given in list - II below

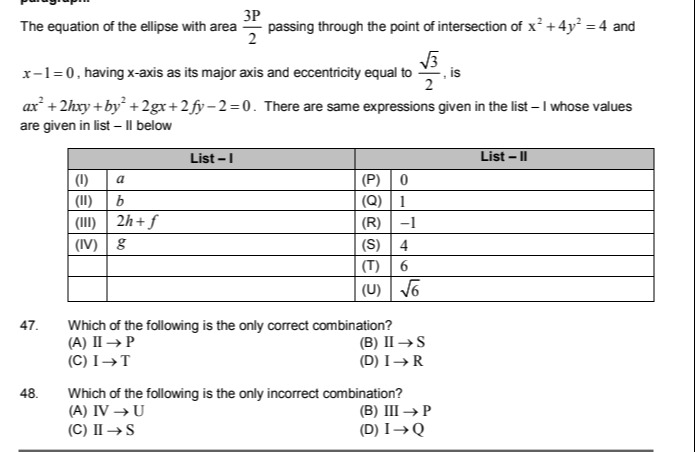
• A. II → P
• B. II → S
• C. I → T
• D. I → R

Answer 1

Answer: (B)

II → S

Answer 2

To solve the problem, we need to find the equation of the ellipse and then identify the values of the coefficients $a, b, h, f, g$.

1. Find the point(s) of intersection: The given equations are $x^2 + 4y^2 = 4$ and $x - 1 = 0$. From $x - 1 = 0$, we get $x = 1$. Substitute $x = 1$ into the first equation: $(1)^2 + 4y^2 = 4$ $1 + 4y^2 = 4$ $4y^2 = 3$ $y^2 = \frac{3}{4}$ $y = \pm \frac{\sqrt{3}}{2}$ So, the ellipse passes through the points $(1, \frac{\sqrt{3}}{2})$ and $(1, -\frac{\sqrt{3}}{2})$.

2. Determine the standard form of the ellipse equation: The x-axis is stated as the major axis, and the ellipse passes through points symmetric with respect to the x-axis. This implies the center of the ellipse lies on the x-axis, so its y-coordinate is 0. Let the center of the ellipse be $(h_0, 0)$. The standard equation of such an ellipse is $\frac{(x-h_0)^2}{a_0^2} + \frac{y^2}{b_0^2} = 1$, where $a_0$ is the semi-major axis and $b_0$ is the semi-minor axis, with $a_0 > b_0$.

3. Use the eccentricity information: The eccentricity $e = \frac{\sqrt{3}}{2}$. For an ellipse with the major axis along the x-axis, the relationship between $a_0, b_0,$ and $e$ is $b_0^2 = a_0^2(1-e^2)$. $b_0^2 = a_0^2 \left(1 - \left(\frac{\sqrt{3}}{2}\right)^2\right)$ $b_0^2 = a_0^2 \left(1 - \frac{3}{4}\right)$ $b_0^2 = a_0^2 \left(\frac{1}{4}\right)$ So, $b_0 = \frac{a_0}{2}$.

4. Use the area information: The area of an ellipse is $\pi a_0 b_0$. The problem states the area is $\frac{3P}{2}$. Given the options for coefficients are simple integers, it is highly probable that 'P' is a typo for '$\pi$'. Thus, we assume Area = $\frac{3\pi}{2}$. $\pi a_0 b_0 = \frac{3\pi}{2}$ $a_0 b_0 = \frac{3}{2}$ Substitute $b_0 = \frac{a_0}{2}$: $a_0 \left(\frac{a_0}{2}\right) = \frac{3}{2}$ $\frac{a_0^2}{2} = \frac{3}{2}$ $a_0^2 = 3$ So, $a_0 = \sqrt{3}$. Then $b_0 = \frac{\sqrt{3}}{2}$, and $b_0^2 = \frac{3}{4}$.

5. Use the passing point to find the center: The ellipse passes through $(1, \frac{\sqrt{3}}{2})$. Substitute this point and the values of $a_0^2$ and $b_0^2$ into the ellipse equation: $\frac{(1-h_0)^2}{a_0^2} + \frac{(\frac{\sqrt{3}}{2})^2}{b_0^2} = 1$ $\frac{(1-h_0)^2}{3} + \frac{\frac{3}{4}}{\frac{3}{4}} = 1$ $\frac{(1-h_0)^2}{3} + 1 = 1$ $\frac{(1-h_0)^2}{3} = 0$ $(1-h_0)^2 = 0$ $h_0 = 1$ So, the center of the ellipse is $(1, 0)$.

6. Write the equation of the ellipse: Substitute $h_0=1$, $a_0^2=3$, and $b_0^2=\frac{3}{4}$ into the standard form: $\frac{(x-1)^2}{3} + \frac{y^2}{\frac{3}{4}} = 1$ $\frac{(x-1)^2}{3} + \frac{4y^2}{3} = 1$ Multiply the entire equation by 3: $(x-1)^2 + 4y^2 = 3$ Expand $(x-1)^2$: $x^2 - 2x + 1 + 4y^2 = 3$ Rearrange the terms to match the given form $ax^2 + 2hxy + by^2 + 2gx + 2fy - 2 = 0$: $x^2 + 4y^2 - 2x + 1 - 3 = 0$ $x^2 + 4y^2 - 2x - 2 = 0$

7. Identify the coefficients: Compare $x^2 + 4y^2 - 2x - 2 = 0$ with $ax^2 + 2hxy + by^2 + 2gx + 2fy - 2 = 0$: $a = 1$ $2h = 0 \implies h = 0$ $b = 4$ $2g = -2 \implies g = -1$ $2f = 0 \implies f = 0$ The constant term $-2$ matches.

8. Match List-I expressions with List-II values: From our calculations: (I) $a = 1$ (II) $b = 4$ (III) $2h + f = 2(0) + 0 = 0$ (IV) $g = -1$

Matching these with List-II: (I) $a = 1 \implies$ (Q) (II) $b = 4 \implies$ (S) (III) $2h + f = 0 \implies$ (P) (IV) $g = -1 \implies$ (R)

---

For Question 47: Which of the following is the only correct combination? (A) II → P: $b=0$. Our calculation $b=4$. Incorrect. (B) II → S: $b=4$. Our calculation $b=4$. Correct. (C) I → T: $a=6$. Our calculation $a=1$. Incorrect. (D) I → R: $a=-1$. Our calculation $a=1$. Incorrect.

The only correct combination is (B).