Question

The equation of the ellipse whose equation of directrix is$3x + 4y - 5 = 0$, coordinates of the focus are$\left( {1,2} \right)$and the eccentricity is $\dfrac{1}{2}$is$91{x^2} + 84{y^2} - 24xy - 170x - 360y + 475 = 0$.
A. True
B. False

Answer 1

Here, in the given question, focus, directrix$ax + by + c = 0$and eccentricity$e$of an ellipse is given. And we are asked to find the equation of an ellipse using its focus, directrix and eccentricity and to match with the given equation, if it is true or not. Let us first understand the concept of ellipse by its definition, which says, An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points(focus) in the plane is constant.

Formula used:
Distance between two points$\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right)$ is given by$\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Perpendicular distance between a point$\left( {{x_0},{y_0}} \right)$ and a line$Ax + By + C = 0$ is calculated by$\dfrac{{\left| {A{x_0} + B{y_0} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

Complete step-by-step answer:
Given, of an ellipse,
Equation of directrix=$3x + 4y - 5 = 0$
Focus$\left( {1,2} \right)$, and
Eccentricity$\left( e \right)$ =$\dfrac{1}{2}$
Let$S\left( {1,2} \right)$be the focus and$DD'$be the directrix and$$$$be any point on the ellipse such that$PM$be the perpendicular on the directrix.
Then, by definition of eccentricity,

$$e = \dfrac{{SP}}{{PM}} \\\ \Rightarrow SP = e \times PM \\\$$

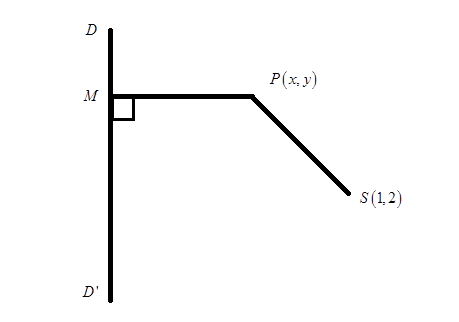
$SP$is the distance between the general point$P\left( {h,k} \right)$and the focus$S\left( {1,2} \right)$which is calculated by $$PM$$is the perpendicular distance between the general point$$P\left( {h,k} \right)$$and the directrix$$3x + 4y - 5 = 0$$, which is calculated by,
Now, we have$SP = e \times PM$

$$Taking square both sides,$$

Simplifying it, we get,

Multiplying$$100$$both sides, $$ 100{x^2} + 500 - 200x + 100{y^2} - 400y = 9{x^2} + 16{y^2} + 24xy + 25 - 30x - 40y \\\ \Rightarrow 91{x^2} + 84{y^2} - 24xy - 170x - 360y + 475 = 0 \\\ $$ Hence, the given statement is true **So, the correct answer is “Option A”.** **Note:** Equation of an ellipse in its standard form with centre$$\left( {h,k} \right)$$and major axis parallel to$$x - axis$$is$$\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$$, where, $$a > b$$ Length of major axis =$$2a$$ Coordinates of the vertices are$$\left( {h \pm a,k} \right)$$ Length of minor axis =$$2b$$ Coordinates of the co-vertices are$$\left( {h,k \pm b} \right)$$ Coordinates of the foci are$$\left( {h \pm c,k} \right)$$, where$${c^2} = {a^2} - {b^2}$$