Question

The equation of the common tangent touching the circle ${\left( {x - 3} \right)^2} + {y^2} = 9$ and the parabola ${y^2} = 4x$ above the x – axis is-
$A\sqrt 2 y = 3x + 1$
$B\sqrt 3 y = - \left( {x + 3} \right)$
$C\sqrt 3 y = x + 3$
$D\sqrt 3 y = - \left( {3x + 1} \right)$

Answer 1

Hint – Here we will proceed by using the common tangent to the parabola such that we can equate it with radius. Then we will solve it by simplifying the equation to get the slope along with the required result.

Complete step-by-step answer:

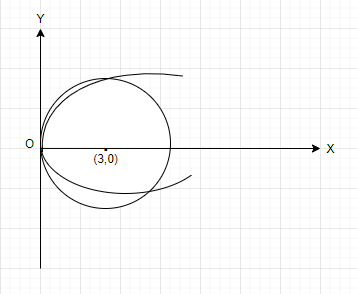
Let the common tangent to the parabola be ${y^2} = 4x$
Now equation of the tangent for the parabola ${y^2} = 4x$ is given by
$y = mx + \dfrac{1}{m}$
It should also touch the circle ${\left( {x - 3} \right)^2} + {y^2} = 9$
By using perpendicular from circle whose centre is (3,0) and radius = 3
Then $\left| {\dfrac{{3m + \dfrac{1}{m}}}{{\sqrt {1 + {m^2}} }}} \right| = 3$
Squaring both sides, we get
$\Rightarrow 9{m^2} + \dfrac{1}{{{m^2}}} + 6$
$\Rightarrow 9 + 9{m^2}$
$\Rightarrow \dfrac{1}{{{m^2}}} = 3$
$\Rightarrow m = \pm \dfrac{1}{{\sqrt 3 }}$
Since the tangent is above the x – axis, we will take a positive slope.
Then equation of common tangent is-
$\Rightarrow y = \dfrac{1}{{\sqrt 3 }}x + \sqrt 3$
Also we can rewrite it as –
$\sqrt 3 y = x + 3$
$\therefore$ Option C is right.

Note – In order to solve this type of question, we must understand the difference between the tangent above the axis or below the axis. If the tangent is above the x – axis, then we will take a positive slope or if the tangent is below the axis then we will take a negative slope.