Question

The equation of the circumcircle of the triangle formed by the lines $x = 0 , y = 0,2 x + 3 y = 5$ is .

• A. $x ^ { 2 } + y ^ { 2 } + 2 x + 3 y - 5 = 0$
• B. $6 \left( x ^ { 2 } + y ^ { 2 } \right) - 5 ( 3 x + 2 y ) = 0$
• C. $x ^ { 2 } + y ^ { 2 } - 2 x - 3 y + 5 = 0$
• D. $6 \left( x ^ { 2 } + y ^ { 2 } \right) + 5 ( 3 x + 2 y ) = 0$

Answer 1

Answer: (B)

$6 \left( x ^ { 2 } + y ^ { 2 } \right) - 5 ( 3 x + 2 y ) = 0$

Answer 2

Given, triangle formed by the lines $x = 0$, $y = 0$, $2 x + 3 y = 5$, so vertices of the triangle are (0, 0), (5/2, 0) and (0, 5/3).

Since circle is passing through (0, 0).

$\therefore$Equation of circle will be $x ^ { 2 } + y ^ { 2 } + 2 g x + 2 f y = 0$ ..(i)

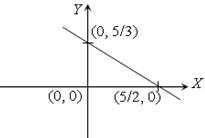
Also, circle is passing through (5/2, 0) and (0, 5/3)

So, $g = - 5 / 4$, $f = - 5 / 6$ .

Put the values of g and f in equation (i).

After solving, we get $6 \left( x ^ { 2 } + y ^ { 2 } \right) - 5 ( 3 x + 2 y ) = 0$, which is the required equation of the circle.